Uma equação é de segundo grau se e somente se pode ser escrita na seguinte forma:
\[ a x ^ 2 + b x + c = 0 \quad , \quad a \neq 0 \]
denominada forma canónica. Os números reais \( a , b \) e \( c \) recebem o nome de coeficiente quadrático, linear e termo independente.
Pode-se sempre supor que o coeficiente quadrático seja maior que zero. Com efeito, no caso em que \( a < 0 \), basta multiplicar ambos os membros por \( -1 \) para reduzir-se ao caso \( a > 0 \).
Índice
- Completar o Quadrado
- Fórmula Reduzida
- Equações de Segundo Grau Monómias
- Equações de Segundo Grau Puras
- Equações de Segundo Grau Incompletas
- Relação entre Soma e Produto das Raízes
- Exercícios Resolvidos
- Significado Geométrico
Completar o Quadrado
Nesta secção deduziremos a fórmula geral para resolver qualquer equação de segundo grau. Partimos da forma canónica:
\[ ax^2 + bx + c = 0, \quad a \neq 0 \]
Para simplificar os cálculos, dividimos tudo por \( a \), de modo a tornar o coeficiente do termo quadrático igual a 1:
\[ x^2 + \frac{b}{a}x + \frac{c}{a} = 0 \]
Agora, isolamos o termo independente passando-o para o segundo membro:
\[ x^2 + \frac{b}{a}x = -\frac{c}{a} \]
Neste ponto, aplicamos o método de completar o quadrado. O truque consiste em adicionar e subtrair uma quantidade para transformar o primeiro membro num quadrado perfeito. Neste caso, o termo em falta é
\[ \left(\frac{b}{2a}\right)^2 \]
Adicionemo-lo a ambos os membros:
\[ x^2 + \frac{b}{a}x + \left(\frac{b}{2a}\right)^2 = -\frac{c}{a} + \left(\frac{b}{2a}\right)^2 \]
O primeiro membro é agora o quadrado de um binómio, pelo que podemos escrevê-lo como
\[ \left(x + \frac{b}{2a}\right)^2 = \frac{b^2}{4a^2} - \frac{4ac}{4a^2} \]
Reescrevemos o segundo membro com denominador comum:
\[ \left(x + \frac{b}{2a}\right)^2 = \frac{b^2 - 4ac}{4a^2} \]
Agora podemos extrair a raiz quadrada de ambos os membros, lembrando que \( \sqrt{x^2} = |x| \):
\[ \left| x + \frac{b}{2a} \right| = \frac{\sqrt{b^2 - 4ac}}{2a} \]
Daqui obtemos diretamente \( x \):
\[ x + \frac{b}{2a} = \pm \frac{\sqrt{b^2 - 4ac}}{2a} \]
Finalmente, isolamos \( x \) e obtemos a célebre fórmula resolutiva:
\[ x_{1,2} = -\frac{b}{2a} \pm \frac{\sqrt{b^2 - 4ac}}{2a} \]
O termo sob a raiz, conhecido como discriminante e indicado com \( \Delta \), é definido como:
\[ \Delta = b^2 - 4ac \]
Mas o que representa o discriminante? Permite-nos determinar num relance o tipo de soluções que a equação terá. Analisemo-lo nos três casos possíveis:
- \( \Delta > 0 \): o discriminante é positivo, pelo que a raiz é um número real. Isto significa que a equação tem duas soluções reais e distintas.
- \( \Delta = 0 \): a raiz quadrada de zero é zero, pelo que a fórmula nos dá uma única solução repetida. Por outras palavras, a equação tem duas soluções coincidentes (ou uma solução dupla).
- \( \Delta < 0 \): a raiz de um número negativo não é um número real, pelo que a equação não tem soluções reais, mas duas soluções complexas com parte imaginária.
Isto significa que, observando apenas o valor de \( \Delta \), podemos prever a natureza das soluções sem necessidade de resolver diretamente a equação.
Fórmula Reduzida
A fórmula reduzida é uma versão simplificada da fórmula resolutiva das equações de segundo grau, útil quando o coeficiente \( b \) é par.
Consideremos uma equação de segundo grau na forma canónica:
\[ ax^2 + bx + c = 0 \]
Se o coeficiente \( b \) é par, podemos escrevê-lo como:
\[ b = 2k \]
Substituindo na equação obtemos:
\[ ax^2 + 2kx + c = 0 \]
A fórmula resolutiva clássica é:
\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
Substituindo \( b = 2k \):
\[ x = \frac{-2k \pm \sqrt{(2k)^2 - 4ac}}{2a} \]
\[ x = \frac{-2k \pm \sqrt{4k^2 - 4ac}}{2a} \]
\[ x = \frac{-2k \pm 2\sqrt{k^2 - ac}}{2a} \]
Dividindo numerador e denominador por 2:
\[ x = \frac{-k \pm \sqrt{k^2 - ac}}{a} \]
Finalmente, podemos expressar a fórmula reduzida como:
\[ x = \frac{-\frac{b}{2} \pm \sqrt{\left(\frac{b}{2}\right)^2 - ac}}{a} \]
O discriminante reduzido é dado por:
\[ \Delta' = \left(\frac{b}{2}\right)^2 - ac \]
Agora comparemo-lo com o discriminante da fórmula completa:
\[ \Delta = b^2 - 4ac \]
Substituindo \( b = 2k \), obtemos:
\[ \Delta = (2k)^2 - 4ac \]
\[ \Delta = 4k^2 - 4ac \]
Dividindo tudo por 4:
\[ \frac{\Delta}{4} = k^2 - ac \]
Visto que \( k = \displaystyle \frac{b}{2} \), podemos reescrever:
\[ \frac{\Delta}{4} = \left(\frac{b}{2}\right)^2 - ac \]
que é exatamente a definição de \( \Delta' \).
Portanto, podemos concluir que:
\[ \Delta' = \frac{\Delta}{4} \]
Equações de Segundo Grau Monómias
Uma equação diz-se monómia se se reduz a um único termo quadrático, ou seja, da forma:
\[ ax^2 = 0 \]
Para resolver esta equação, dividimos ambos os membros por \( a \) (supondo \( a \neq 0 \)):
\[ x^2 = 0 \]
Extraindo a raiz quadrada, obtemos a solução:
\[ x = 0 \]
Embora o valor seja único, matematicamente consideram-se duas soluções coincidentes: \( x_1 = x_2 = 0 \).
Equações de Segundo Grau Puras
Uma equação diz-se pura se, na forma geral \( ax^2 + bx + c = 0 \), o coeficiente \( b \) é nulo, reduzindo-se a:
\[ ax^2 + c = 0 \]
Para resolver esta equação, passamos o termo independente \( c \) para o segundo membro:
\[ ax^2 = -c \]
Dividimos ambos os membros por \( a \neq 0 \):
\[ x^2 = -\frac{c}{a} \]
As soluções existem apenas se \( \displaystyle -\frac{c}{a} \geq 0 \), caso contrário a equação não tem soluções reais. Se o valor sob a raiz é positivo, obtemos:
\[ x_{1,2} = \pm \sqrt{-\frac{c}{a}} \]
Equações de Segundo Grau Incompletas
Uma equação diz-se incompleta se o termo independente é nulo, ou seja:
\[ ax^2 + bx = 0 \]
Neste caso, podemos resolvê-la fatorando \( x \) como fator comum:
\[ x (ax + b) = 0 \]
Aplicando a lei de anulação do produto, obtemos as duas soluções:
\[ x = 0 \quad \text{ou} \quad x = -\frac{b}{a} \]
Relação entre Soma e Produto das Raízes
Consideremos a equação quadrática do tipo \( ax^2 + bx + c = 0 \), onde \( a \), \( b \) e \( c \) são os coeficientes. Sejam \( x_1 \) e \( x_2 \) as raízes desta equação. Agora, queremos escrever a equação em termos das raízes. Uma equação de segundo grau pode ser escrita como o produto dos fatores \( (x - x_1) \) e \( (x - x_2) \), portanto podemos escrever:
\[ a(x - x_1)(x - x_2) = 0 \]
Desenvolvendo o produto à esquerda, obtemos:
\[ a(x^2 - (x_1 + x_2)x + x_1x_2) = 0 \]
Agora, pela propriedade distributiva, obtemos:
\[ ax^2 - a(x_1 + x_2)x + ax_1x_2 = 0 \]
Neste ponto, podemos comparar esta expressão com a equação canónica \( ax^2 + bx + c = 0 \). Em particular, vemos que os coeficientes devem ser iguais. Comparando o termo linear, obtemos:
\[ -a(x_1 + x_2) = b \]
Resolvendo para \( x_1 + x_2 \), obtemos:
\[ x_1 + x_2 = -\frac{b}{a} \]
Do mesmo modo, comparando o termo constante, obtemos:
\[ ax_1x_2 = c \]
Resolvendo para o produto das raízes, obtemos:
\[ x_1 \cdot x_2 = \frac{c}{a} \]
Em síntese, as raízes \( x_1 \) e \( x_2 \) estão relacionadas com os coeficientes \( a \), \( b \) e \( c \) através destas duas relações simples: a soma das raízes é \( \displaystyle -\frac{b}{a} \) e o produto das raízes é \( \displaystyle \frac{c}{a} \). Estas propriedades são fundamentais e permitem-nos deduzir informações importantes sobre as raízes sem as calcular diretamente.
Exercícios Resolvidos
Exercício 1. Resolver a equação de segundo grau \( x^2 - 3x - 5 = 0 \).
Solução. Para a resolver, utilizamos a seguinte fórmula:
\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
Neste caso, os coeficientes são \( a = 1 \), \( b = -3 \) e \( c = -5 \). Aplicando a fórmula:
\[ x = \frac{-(-3) \pm \sqrt{(-3)^2 - 4(1)(-5)}}{2(1)} = \frac{3 \pm \sqrt{9 + 20}}{2} = \frac{3 \pm \sqrt{29}}{2} \]
As soluções são portanto:
\[ x_1 = \frac{3 + \sqrt{29}}{2} \quad , \quad x_2 = \frac{3 - \sqrt{29}}{2} \]
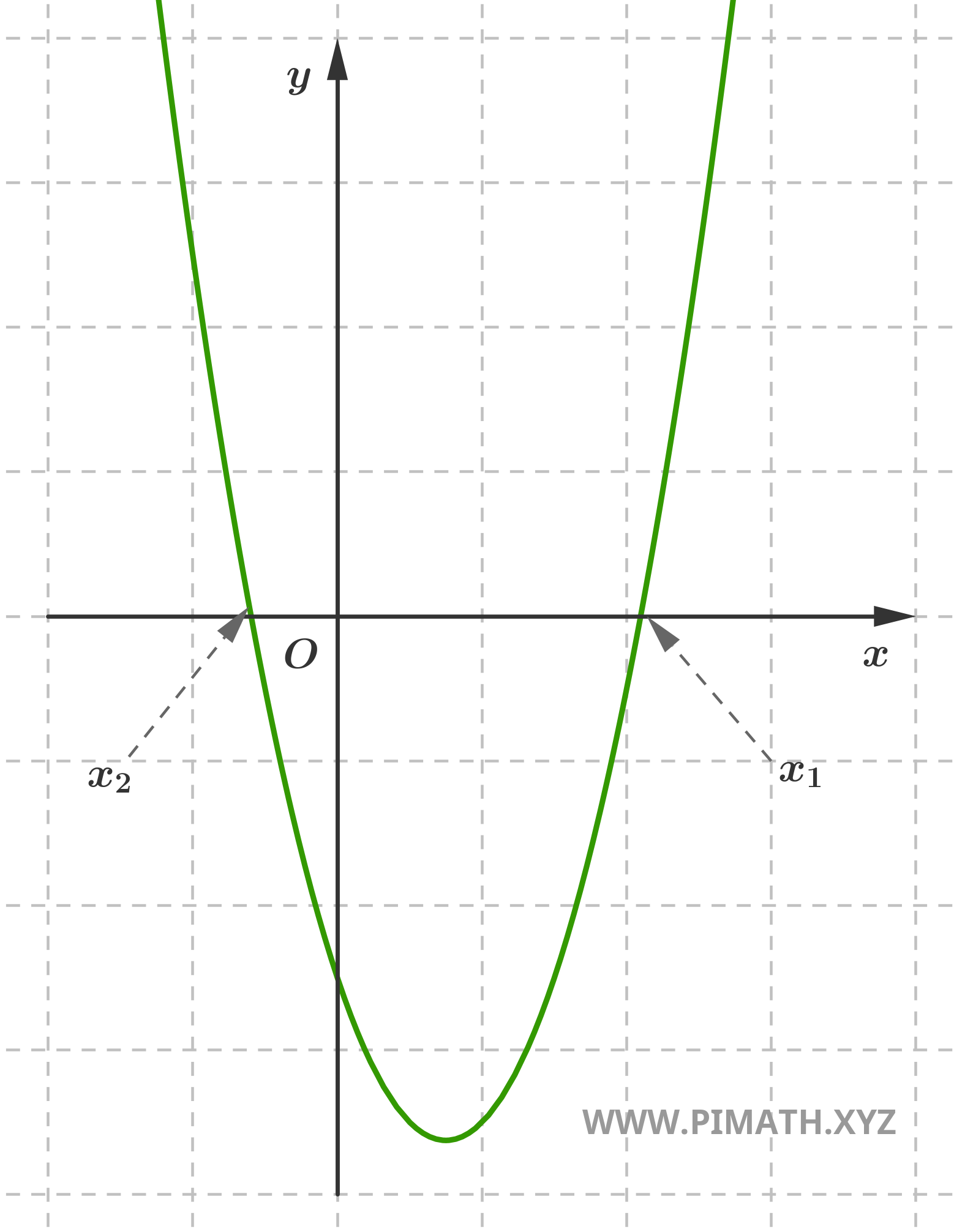
Exercício 2 (forma reduzida). Encontrar as soluções da seguinte equação \( x^2 + 6x = 0 \).
Solução. Para a resolver, podemos fatorar o fator comum:
\[ x(x + 6) = 0 \]
As soluções são portanto: \( x_1 = 0 \) e \( x_2 = -6 \).
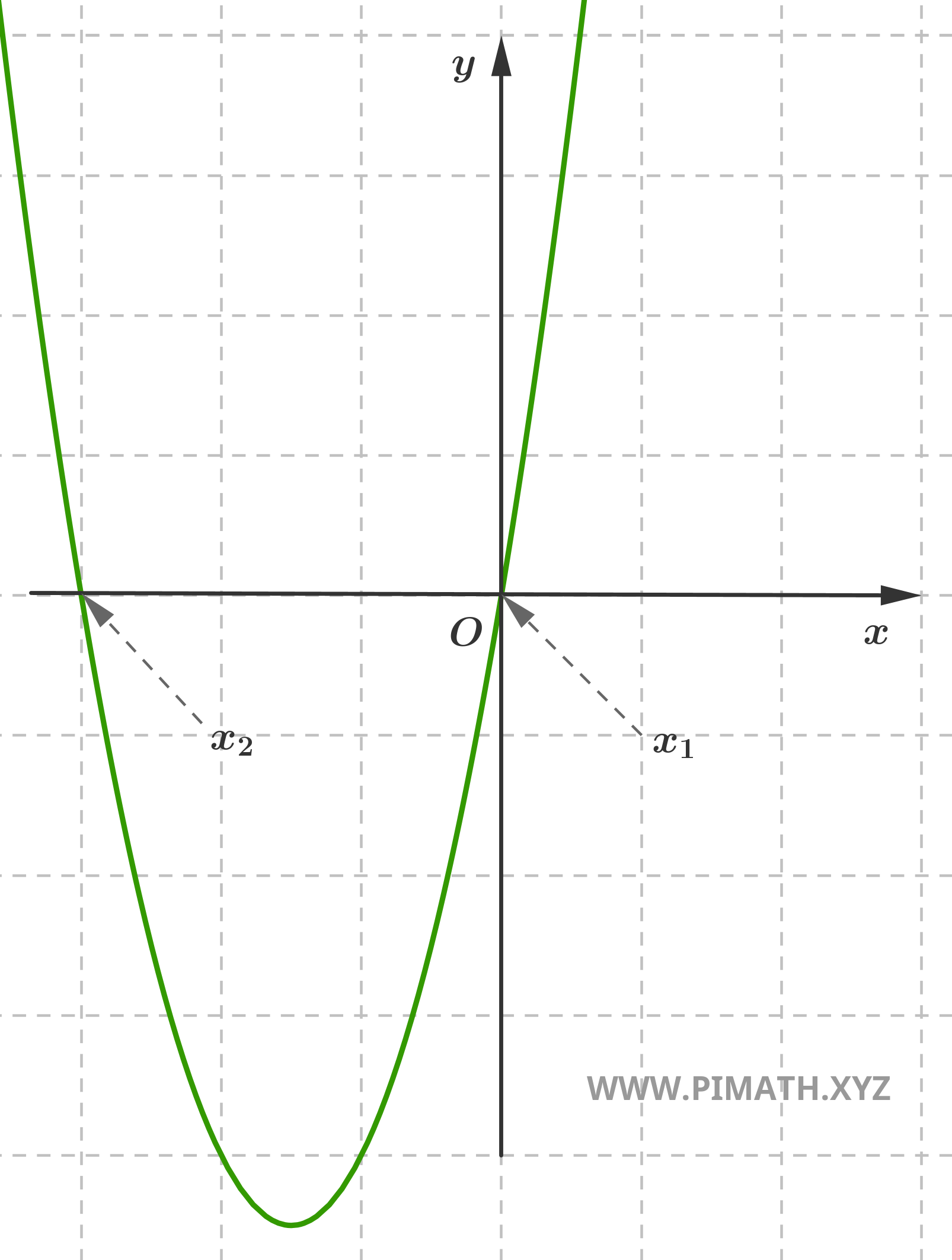
Exercício 3 (equação pura). Encontrar as soluções da equação \( x^2 = 16 \).
Solução. Para a resolver, podemos extrair a raiz quadrada de ambos os membros:
\[ x = \pm \sqrt{16} = \pm 4 \]
As soluções são portanto: \( x_1 = 4 \) e \( x_2 = -4 \).
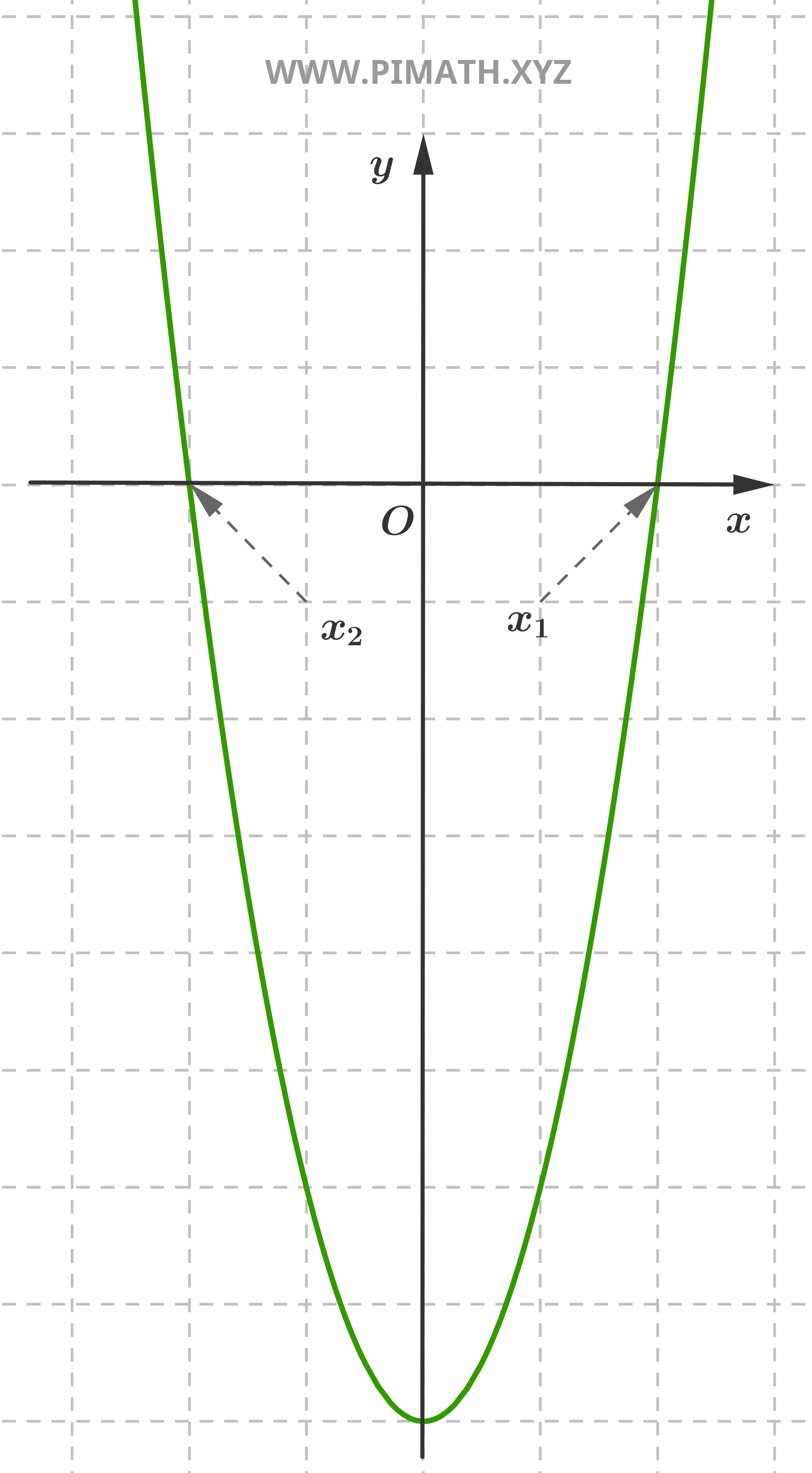
Exercício 4 (equação pura). Encontrar as soluções da equação \( x^2 + 9 = 0 \).
Solução. Isolamos \( x^2 \):
\[ x^2 = -9 \]
Visto que não existem números reais que satisfaçam esta equação, a equação não admite soluções reais.
Exercício 5. Encontrar as soluções da seguinte equação \( x^2 - 4 = 0 \).
Solução. Isolamos \( x^2 \):
\[ x^2 = 4 \]
Agora extraímos a raiz quadrada de ambos os membros:
\[ x = \pm \sqrt{4} = \pm 2 \]
As soluções são portanto:
\[ x_1 = 2 \quad , \quad x_2 = -2 \]
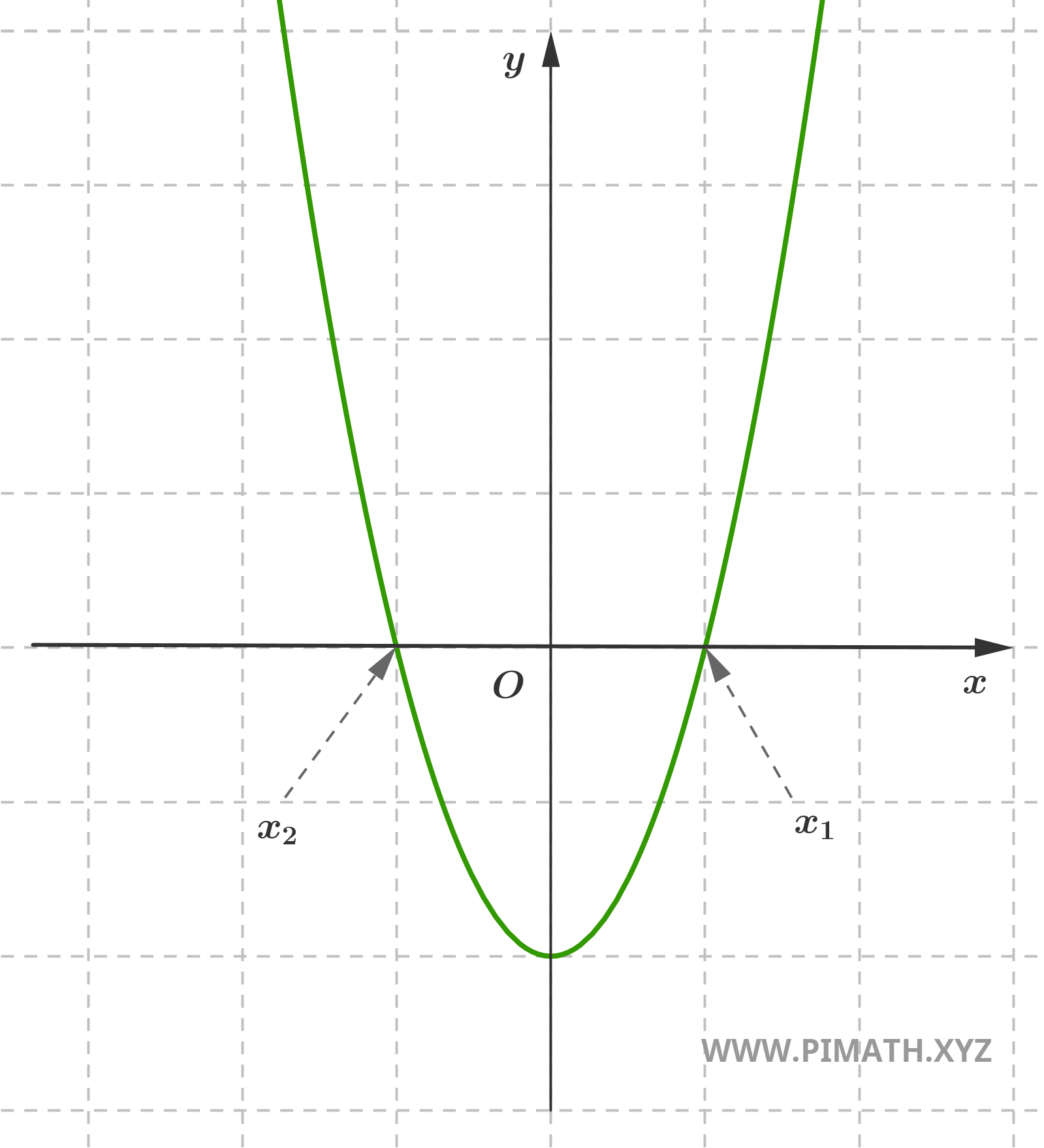
Significado Geométrico
Do ponto de vista geométrico, resolver uma equação de segundo grau significa encontrar os valores reais (se existirem) para os quais a parábola de equação \( y = ax^2 + bx + c \) interseta o eixo das abscissas \( x \) ou, se quisermos, a reta \( y = 0 \).

