Uma equação do primeiro grau é um polinómio do primeiro grau igualado a zero. Em geral, uma equação é do primeiro grau se pode ser escrita na forma canónica:
\[ ax + b = 0 \quad \text{com} \quad a \neq 0 \]
A parte que fica à esquerda do sinal de igualdade denomina-se primeiro membro, enquanto que a que fica à direita denomina-se segundo membro.
Índice
- Como resolver uma equação do primeiro grau
- Primeiro princípio de equivalência
- Segundo princípio de equivalência
- Exercícios Resolvidos
- Erros comuns a evitar
- Significado Geométrico
Como resolver uma equação do primeiro grau
Resolver uma equação do primeiro grau significa encontrar o valor que, substituído na incógnita \( x \), satisfaz a equação. Isto equivale a dizer que o valor (solução da equação) deve tornar verdadeira a igualdade. O processo de resolução prevê alguns passos, denominados princípios de equivalência para as equações.
Primeiro princípio de equivalência
O primeiro princípio de equivalência afirma que, adicionando ou subtraindo a ambos os membros de uma equação uma quantidade ou uma expressão algébrica, o conjunto das soluções não se altera.
Graças a este princípio, podemos subtrair a quantidade \( -b \) a ambos os membros:
\[ ax = -b \]
Note-se que somar ou subtrair uma quantidade a ambos os membros equivale a "transportar" de um membro para o outro, contanto que seja mudado o sinal. Por enquanto transportámos para o segundo membro \( b \) mudado de sinal, portanto \( -b \).
Segundo princípio de equivalência
O segundo princípio de equivalência afirma que, multiplicando ou dividindo por um mesmo número diferente de zero, o conjunto das soluções da equação não se altera.
Aplicando este princípio à equação equivalente \( ax = -b \), portanto dividindo pelo número \( a \neq 0 \) ambos os membros, obtemos:
\[ x = -\frac{b}{a} \]
É importante sublinhar que \( a \) deve ser diferente de zero para que a equação tenha sentido. De facto, se \( a = 0 \) a equação tornar-se-ia \( 0 \cdot x + b = 0 \) e portanto \( b = 0 \), que não representa uma equação em \( x \) e seria impossível se \( b \neq 0 \).
Doravante o objetivo será isolar a variável \( x \) no primeiro membro, ou no segundo (não muda nada).
Exercícios Resolvidos
Exercício 1. Resolver a equação \( 3x - 1 = 0\).
Solução. Transportamos \( -1 \) para o segundo membro (mudando-lhe o sinal):
\[ 3x = 1 \]
Finalmente, dividindo ambos os membros por \( 3 \) obtemos a solução procurada:
\[ x = \frac{1}{3} \]
Verificação. Para verificar que é a solução correta, substituímos o valor encontrado na equação de partida. Obtemos:
\[ 3 \cdot \frac{1}{3} - 1 = 1 - 1 = 0 \]
Portanto a solução está correta.
Exercício 2: Resolver a equação do primeiro grau \(\displaystyle\frac{1}{2}(x-1)=-x+1\).
Solução. Começamos por isolar a incógnita \( x \) no primeiro membro:
\[ \frac{1}{2}(x - 1) = -x + 1 \implies \frac{x}{2} - \frac{1}{2} = -x + 1 \]
Agora somamos \(x\) a ambos os membros da equação:
\[ \frac{x}{2} + x - \frac{1}{2} = 1 \]
Simplificamos transformando \(x\) num termo com denominador comum:
\[ \frac{x}{2} + \frac{2x}{2} - \frac{1}{2} = 1 \implies \frac{3x}{2} - \frac{1}{2} = 1 \]
Adicionamos \(\displaystyle\frac{1}{2}\) a ambos os membros:
\[ \frac{3x}{2} = \frac{3}{2} \]
Agora multiplicamos ambos os membros por \(\displaystyle\frac{2}{3}\) para resolver para \(x\):
\[ x = 1 \]
Portanto, a solução é \( x = 1 \).
Verificação. Como anteriormente, substituímos \( x = 1 \) na equação de partida:
\[ \frac{1}{2}(x - 1) = -x + 1 \]
Quando \( x = 1 \), obtemos:
\[ \frac{1}{2}(1 - 1) = -1 + 1 \]
Calculamos ambos os membros:
\[ \frac{1}{2} \cdot 0 = 0 \quad \text{e} \quad -1 + 1 = 0 \]
Os dois membros são iguais, portanto a solução está correta.
Exercício 3. Resolver a equação \( 5(x - 2) - 3(2x + 1) = 7 - 4x \)
Solução. Aplicamos a propriedade distributiva:
\[ 5x - 10 - 6x - 3 = 7 - 4x \]
\[ -x - 13 = 7 - 4x \]
Transportamos os termos com \(x\) para o primeiro membro e os termos constantes para o segundo membro:
\[ -x + 4x = 7 + 13 \]
\[ 3x = 20 \]
Dividimos ambos os membros por 3:
\[ x = \frac{20}{3} \]
Verificação. Substituímos \(\displaystyle x = \frac{20}{3}\) na equação de partida:
\[ 5\left(\frac{20}{3} - 2\right) - 3\left(2\cdot\frac{20}{3} + 1\right) = 7 - 4\cdot\frac{20}{3} \]
Calculamos o primeiro membro:
\[ 5\left(\frac{20}{3} - \frac{6}{3}\right) - 3\left(\frac{40}{3} + \frac{3}{3}\right) = 5\cdot\frac{14}{3} - 3\cdot\frac{43}{3} = \frac{70}{3} - \frac{129}{3} = -\frac{59}{3} \]
Calculamos o segundo membro:
\[ 7 - 4\cdot\frac{20}{3} = \frac{21}{3} - \frac{80}{3} = -\frac{59}{3} \]
Os dois membros são iguais, portanto a solução está verificada:
\[ x = \frac{20}{3} \]
Erros comuns a evitar
Quando se resolvem equações do primeiro grau, é importante ter atenção a alguns erros frequentes:
Erro na mudança de sinal: Quando se desloca um termo de um membro para o outro, é preciso lembrar de lhe mudar o sinal. Por exemplo, na equação \(2x + 3 = 5\), deslocando o \( 3 \) obtém-se \(2x = 5 - 3\) e não \(2x = 5 + 3\).
Distribuição incompleta: Quando se tem uma expressão do tipo \(3(x + 2)\), o coeficiente \( 3 \) deve ser multiplicado por todos os termos dentro dos parênteses. Um erro comum é escrever \(3x + 2\) em vez do correto \(3x + 6\).
Erros com frações: Quando se tem uma equação como \(\displaystyle \frac{x}{2} = 3\), para isolar \(x\) é preciso multiplicar ambos os membros por 2, obtendo \(x = 6\). É errado escrever \(x = \displaystyle \frac{3}{2}\).
Simplificação imprecisa: Numa equação como \(2x - x = 5\), não se deve esquecer de simplificar os termos semelhantes antes de prosseguir. A forma correta é \(x = 5\).
Verificação em falta: Saltar o passo da verificação pode levar a não se aperceber de eventuais erros de cálculo. É sempre aconselhável substituir a solução encontrada na equação original para confirmar que está correta.
Significado Geométrico
Resolver uma equação do primeiro grau \( ax + b = 0\) significa encontrar o valor em correspondência do qual a reta de equação
\[ y = ax + b \]
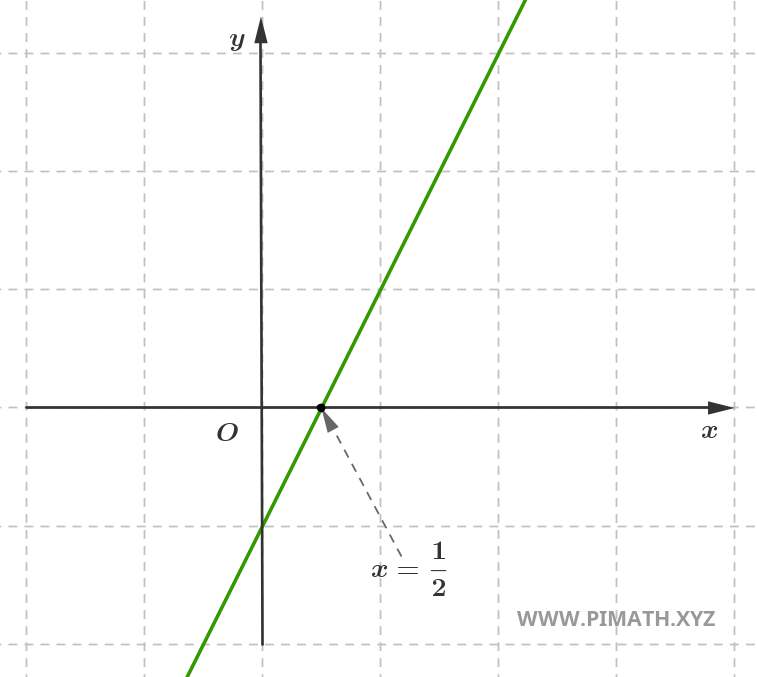
interseta o eixo das abcissas (eixo \( x \)). Por exemplo, a reta de equação \( y = 2x - 1 \)
interseta o eixo das abcissas no ponto \( x = \displaystyle \frac{1}{2} \), como mostrado na figura.
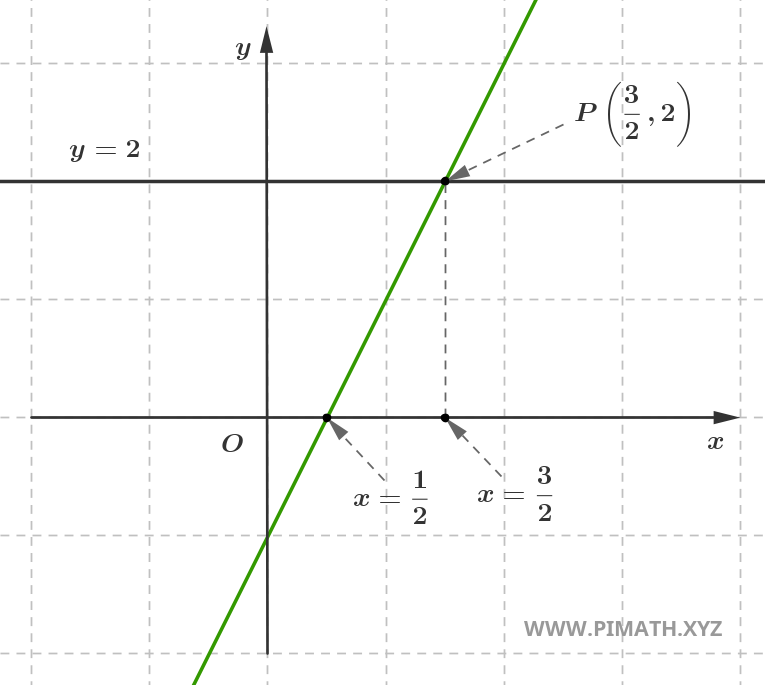
Dissemos que a solução de uma equação do primeiro grau \( ax + b = 0 \) é a abcissa na qual a reta interseta o eixo \(x\). Agora, ponhamos outra questão: como podemos determinar o valor de \( x \) para o qual a reta \( y = ax + b \) assume um valor específico, por exemplo \( y = 2 \)?
Para fazer isto, basta impor \( y = 2 \) na equação da reta. Obtemos assim \( 2 = 2x - 1 \iff 2x - 3 = 0 \), portanto:
\[ x=\frac{3}{2} \]
Como mostrado na figura, à solução que encontrámos corresponde a ordenada \(y=2\).