As funções pares e funções ímpares distinguem-se pelas suas simetrias: as funções pares são simétricas em relação ao eixo das ordenadas, enquanto as funções ímpares o são em relação à origem. Aprofundaremos também o comportamento da soma de funções: a soma de duas funções pares continua a ser uma função par, assim como a soma de duas funções ímpares continua a ser ímpar. Por fim, veremos como decompor uma função na sua parte par e na sua parte ímpar.
- Funções Pares
- Soma de duas funções pares
- Funções Ímpares
- Soma de duas funções ímpares
- Funções que não são nem pares nem ímpares
- Integração em intervalos simétricos
- Decomposição de uma função em parte par e parte ímpar
- Demonstração da unicidade da decomposição
Funções Pares
Definição. Uma função \( f : X \to Y \) diz-se par se:
\[ \forall x \in X, \quad -x \in X \quad \text{e} \quad f(-x) = f(x) \]
Por outras palavras, a função é par se o domínio é simétrico em relação à origem e a função assume o mesmo valor em \( x \) e \( -x \).
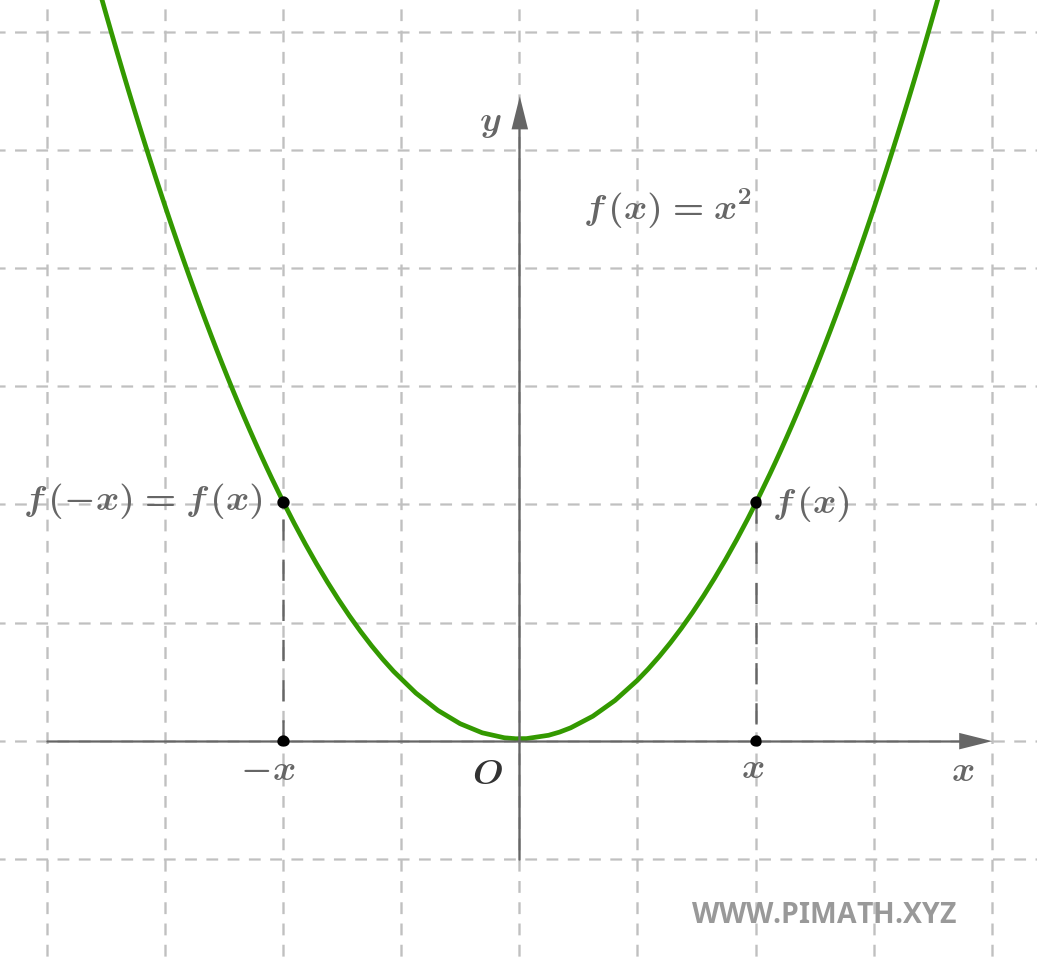
Exemplo. A função \( f(x) = x^2 \) é par, pois para todo \( x \in \mathbb{R} \), tem-se \( (-x)^2 = x^2 \).
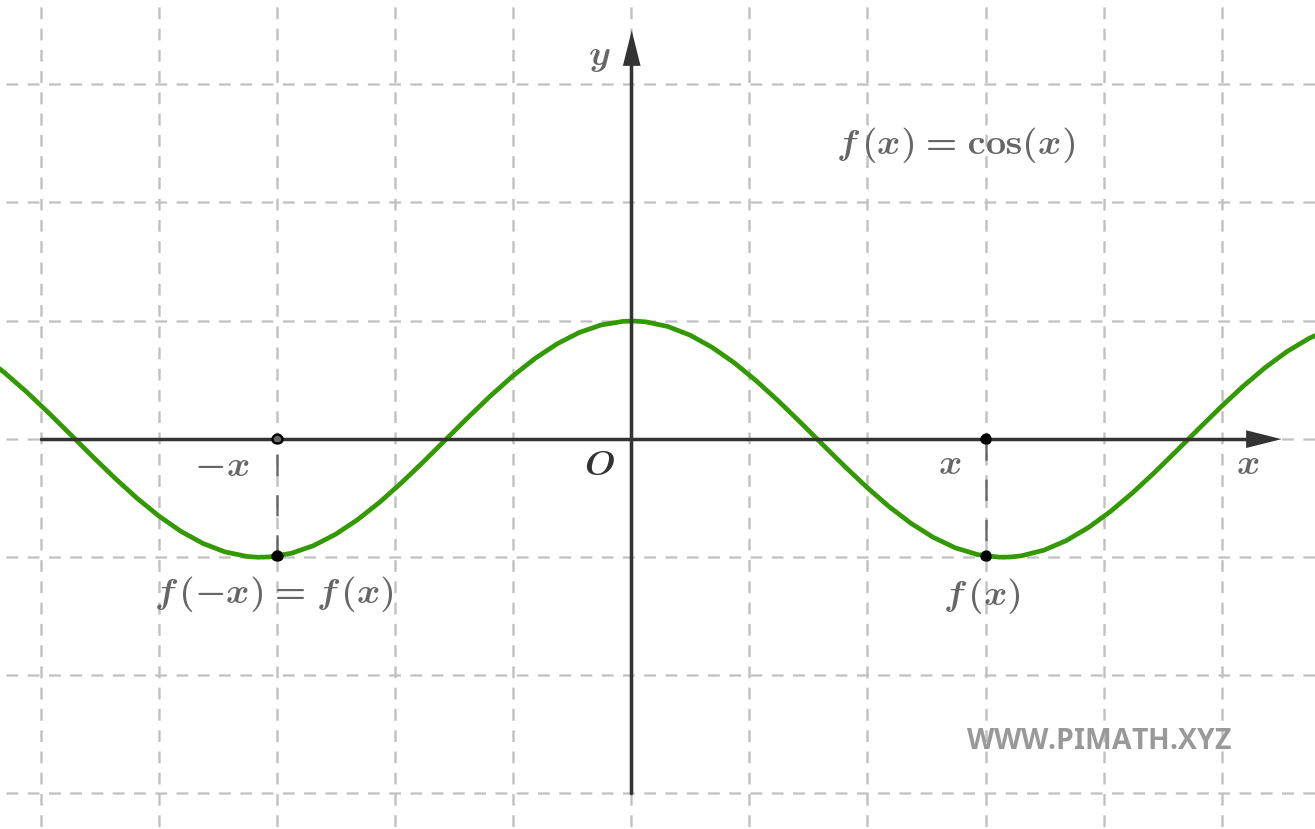
Exemplo. A função \( f(x) = \cos(x) \) é par, pois para todo \( x \in \mathbb{R} \), tem-se \( \cos(-x) = \cos(x) \).
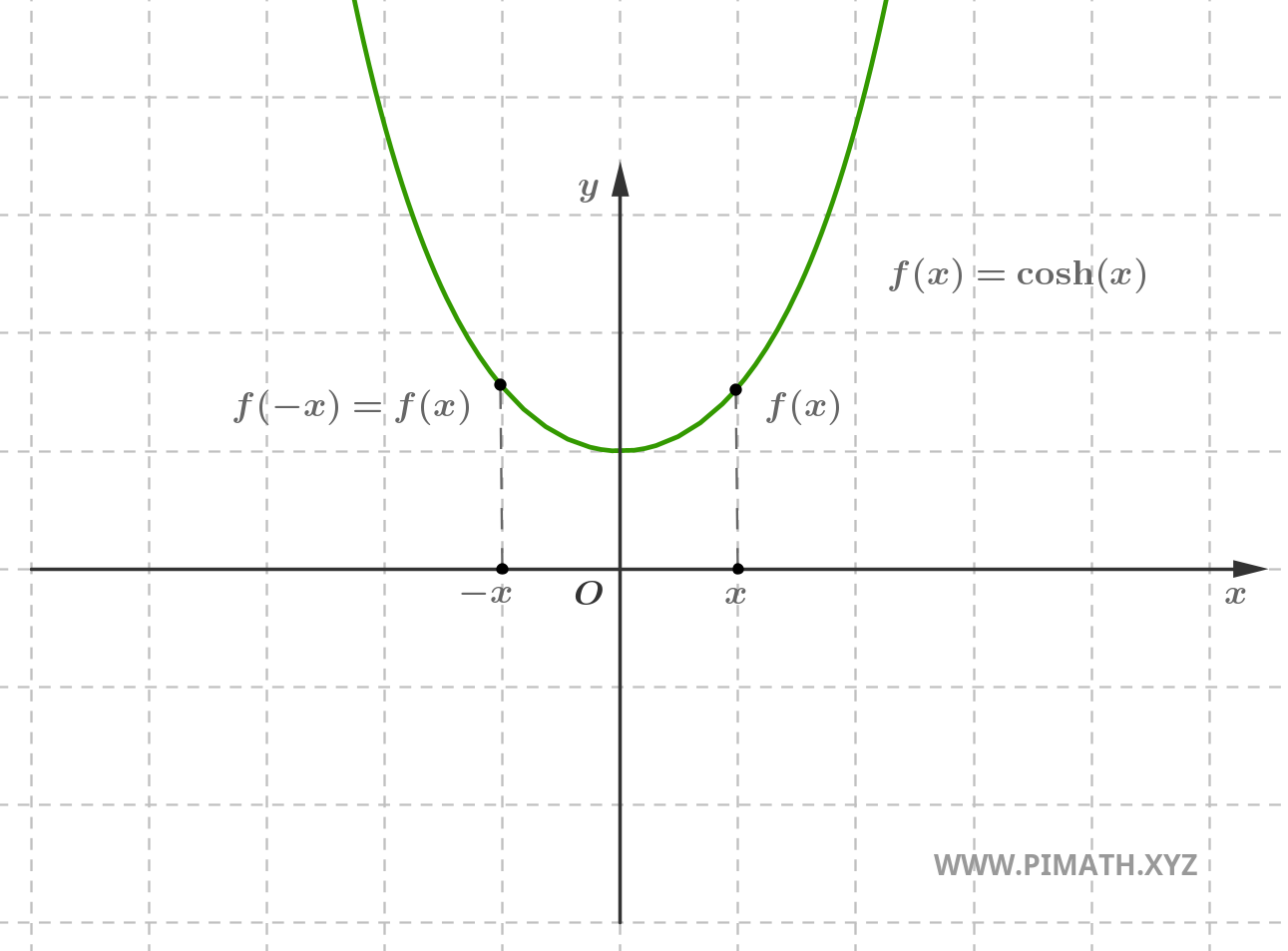
Exemplo. A função \( f(x) = \cosh(x) \) é par, pois para todo \( x \in \mathbb{R} \), tem-se \( \cosh(-x) = \cosh(x) \).
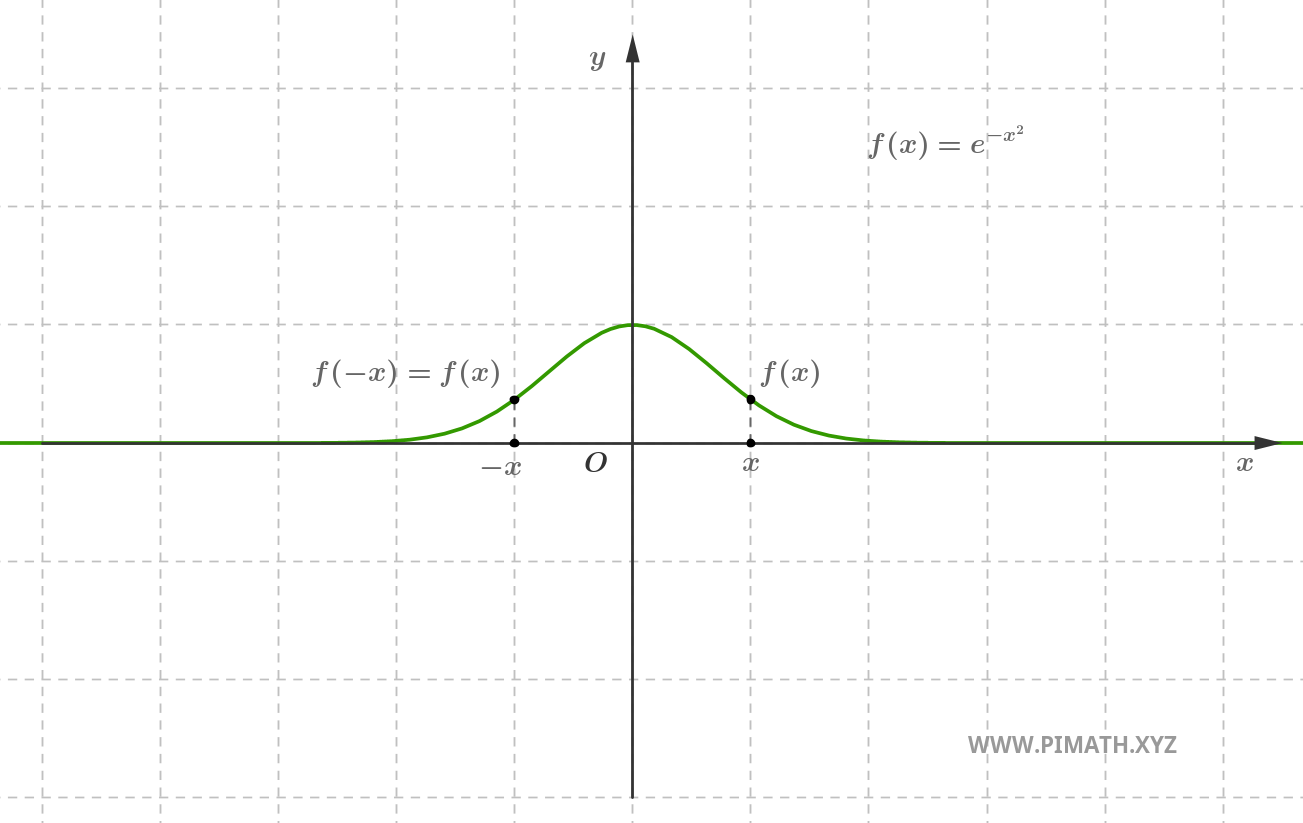
Exemplo. A função \( f(x) = e^{-x^2} \) é par, pois para todo \( x \in \mathbb{R} \), tem-se \( e^{-(-x)^2} = e^{-x^2} \).
Soma de duas funções pares
Sejam \( f \) e \( g \) duas funções pares, definidas respetivamente em \( D_f \) e \( D_g \). Consideremos a função soma \( f + g \), definida no domínio \( D = D_f \cap D_g \). Visto que \( D_f \) e \( D_g \) são simétricos, também a interseção \( D \) é simétrica. Para todo \( x \in D \), temos:
\[ (f + g)(-x) = f(-x) + g(-x) = f(x) + g(x) = (f + g)(x) \]
portanto \( f + g \) é uma função par.
Uma função par apresenta simetria em relação ao eixo das ordenadas. Portanto, para analisar o seu gráfico, é suficiente estudá-la para \( x \geq 0 \); o troço para \( x < 0 \) obtém-se por simetria.
Funções Ímpares
Definição. Uma função \( f : X \to Y \) diz-se ímpar se:
\[ \forall x \in X, \quad -x \in X \quad \text{e} \quad f(-x) = -f(x) \]
Por outras palavras, a função é ímpar se o domínio é simétrico em relação à origem e a função assume valores opostos em \( x \) e \( -x \).
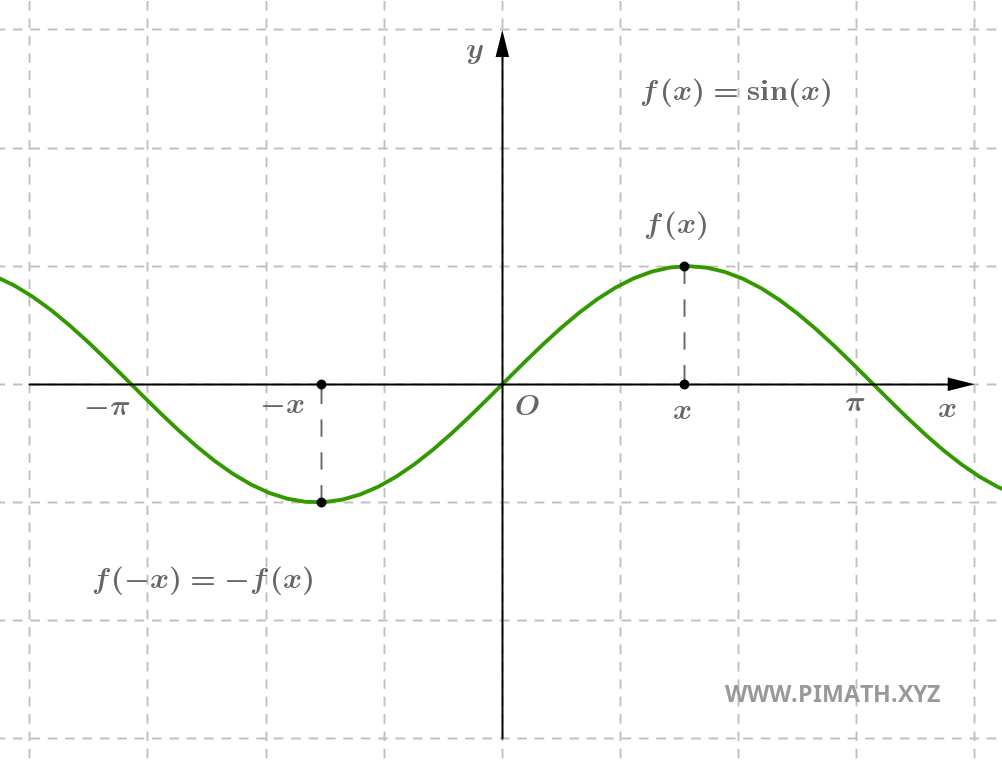
Exemplo. A função \( f(x) = \sin(x) \) é ímpar, pois para todo \( x \in \mathbb{R} \), tem-se \( \sin(-x) = -\sin(x) \).
Exemplo. A função \( f(x) = x^3 \) é ímpar, pois para todo \( x \in \mathbb{R} \), tem-se \( (-x)^3 = -x^3 \).
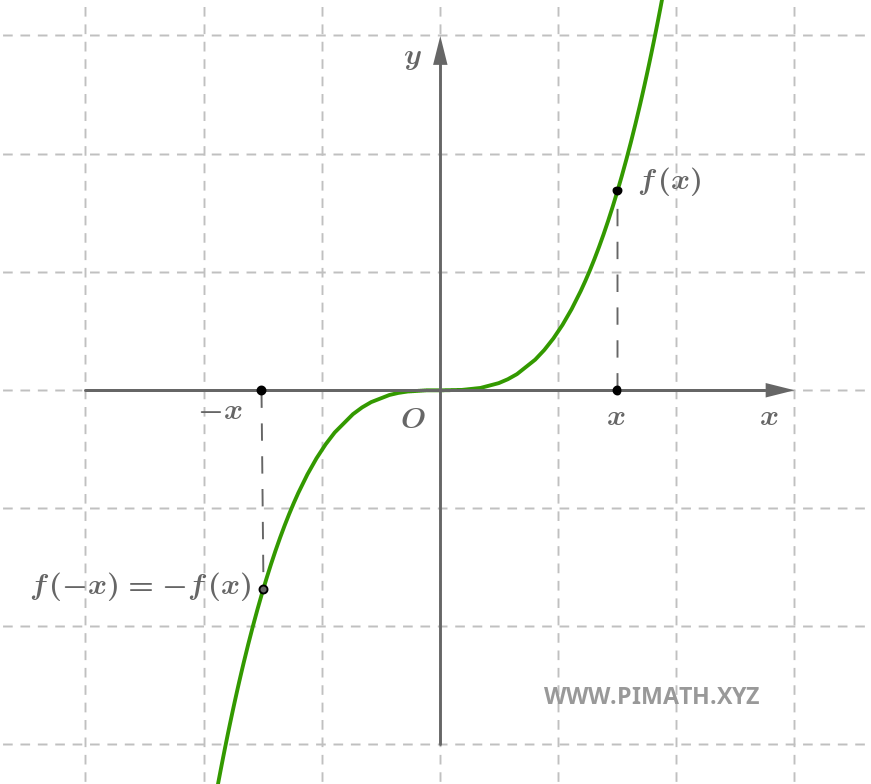
Uma função ímpar é simétrica em relação à origem: rodando o seu gráfico 180° em torno da origem, obtém-se o mesmo gráfico.
Soma de duas funções ímpares
Sejam \( f \) e \( g \) duas funções ímpares, definidas nos domínios \( D_f \) e \( D_g \). Então a soma \( f + g \), definida no domínio comum \( D = D_f \cap D_g \), é também ímpar.
Com efeito, para todo \( x \in D \), vale:
\[ (f + g)(-x) = f(-x) + g(-x) = -f(x) - g(x) = -(f(x) + g(x)) = -(f + g)(x) \]
Portanto, \( f + g \) é uma função ímpar.
Funções que não são nem pares nem ímpares
Se uma função não satisfaz nem a relação \( f(-x) = f(x) \), nem \( f(-x) = -f(x) \), então não é nem par nem ímpar.
Exemplo. As funções \( f(x) = e^x \) e \( f(x) = x + 1 \) não são nem pares nem ímpares.
Integração em intervalos simétricos
As funções pares e ímpares são particularmente úteis no cálculo de integrais definidos em intervalos simétricos em relação à origem.
Se \( f \) é par, então:
\[ \int_{-a}^{a} f(x) \, dx = 2 \int_{0}^{a} f(x) \, dx \]
Se \( f \) é ímpar, então:
\[ \int_{-a}^{a} f(x) \, dx = 0 \]
Decomposição de uma função em parte par e parte ímpar
Seja \( f : X \to \mathbb{R} \) uma função definida num conjunto simétrico em relação à origem, isto é, tal que \( x \in X \implies -x \in X \). Neste caso, a função \( f \) pode ser escrita de modo único como soma de uma função par e de uma função ímpar.
Precisamente, definem-se:
\[ f_p(x) = \frac{f(x) + f(-x)}{2} \quad \text{(parte par de \( f \))} \]
\[ f_i(x) = \frac{f(x) - f(-x)}{2} \quad \text{(parte ímpar de \( f \))} \]
É imediato verificar que \( f_p(-x) = f_p(x) \) e \( f_i(-x) = -f_i(x) \), portanto \( f_p \) é par e \( f_i \) é ímpar. Além disso, somando as duas expressões obtém-se:
\[ f(x) = f_p(x) + f_i(x) \]
isto é, toda a função \( f \) (definida num conjunto simétrico) pode decompor-se de modo único na soma de uma função par e uma ímpar.
Exemplo. Consideremos a função \( f(x) = e^x \), definida em todo o \( \mathbb{R} \). A parte par é:
\[ f_p(x) = \frac{e^x + e^{-x}}{2} = \cosh x \]
enquanto a parte ímpar é:
\[ f_i(x) = \frac{e^x - e^{-x}}{2} = \sinh x \]
Tem-se então a decomposição:
\[ e^x = \cosh x + \sinh x \]
Observação: A decomposição é possível apenas se o domínio da função é simétrico em relação à origem. Além disso, a escrita \( f = f_p + f_i \) é única: existe uma só função par e uma só função ímpar cuja soma devolve \( f \).
Demonstração da unicidade da decomposição
Suponhamos que uma função \( f : X \to \mathbb{R} \), definida num conjunto simétrico em relação à origem, se possa escrever de dois modos distintos como soma de uma função par e de uma função ímpar:
\[ f(x) = f_p(x) + f_i(x) = g_p(x) + g_i(x), \]
onde \( f_p \), \( g_p \) são pares e \( f_i \), \( g_i \) são ímpares.
Então:
\[ f_p(x) - g_p(x) = g_i(x) - f_i(x) \]
Chamemos \( h(x) = f_p(x) - g_p(x) = g_i(x) - f_i(x) \). A função \( h \) é portanto par (como diferença de duas funções pares) e ímpar (como diferença de duas funções ímpares).
Mas se uma função é simultaneamente par e ímpar, então:
\[ h(x) = h(-x) \quad \text{e} \quad h(x) = -h(-x) \implies h(x) = -h(x) \]
isto é, \( h(x) = 0 \) para todo \( x \in X \).
Logo, \( f_p(x) = g_p(x) \) e \( f_i(x) = g_i(x) \), o que demonstra a unicidade da decomposição.