Os limites notáveis são expressões fundamentais em análise matemática que descrevem o comportamento local das funções em pontos críticos.
Estes limites são ferramentas essenciais para estabelecer a continuidade, a diferenciabilidade e para simplificar a análise do comportamento assintótico de funções mais complexas.
- Demonstração pelo Critério de Comparação
- Demonstração pela regra de De L'Hôpital
- Demonstração pela expansão em série de Taylor
Demonstração pelo Critério de Comparação
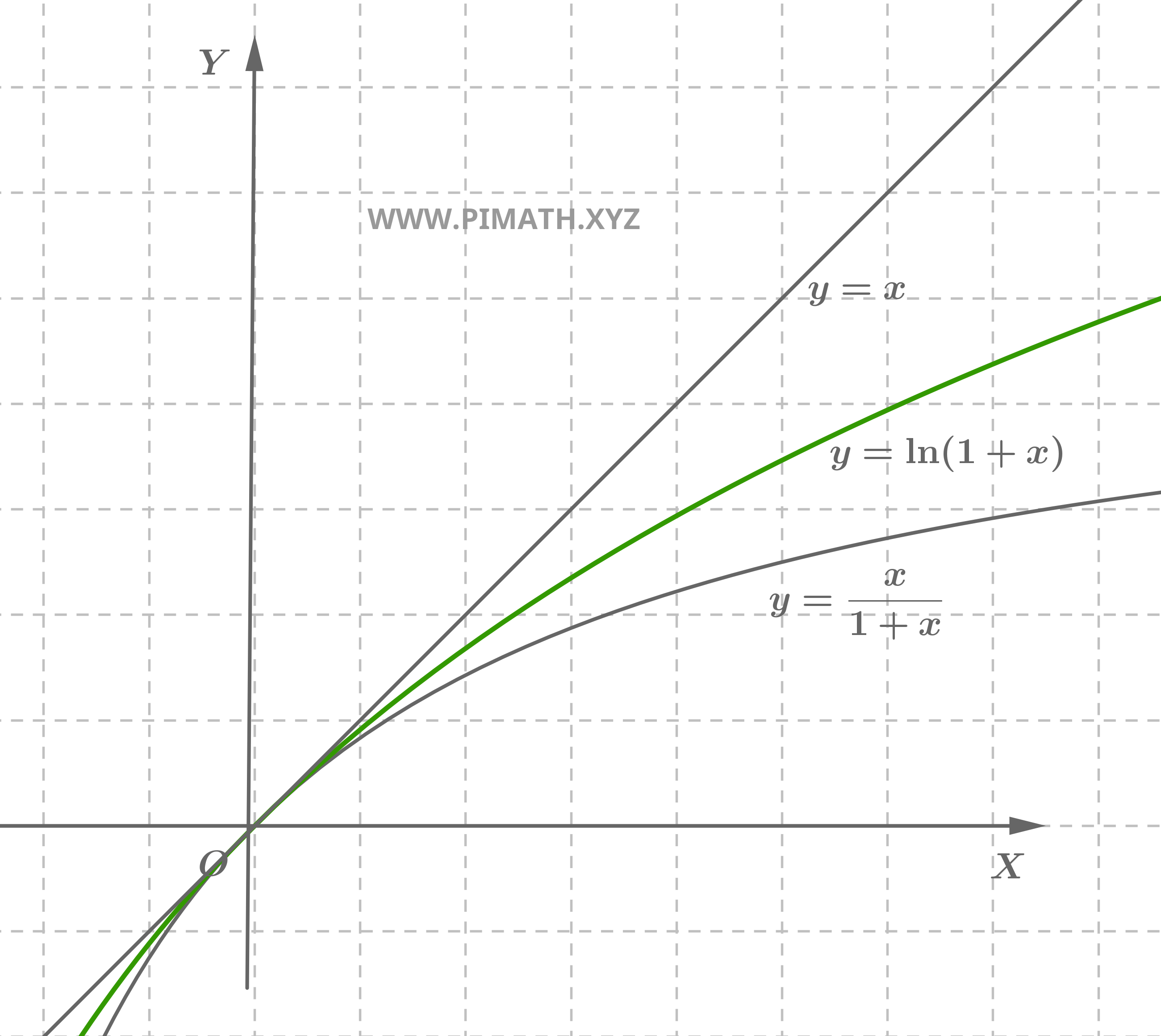
Consideremos o limite \[ \lim_{x \to 0} \frac{\ln(1+x)}{x}. \] Para \( x > 0 \) podemos utilizar as propriedades de concavidade da função \(\ln(1+x)\). Em particular, sabendo que a função é côncava, resulta que o gráfico de \(\ln(1+x)\) situa-se abaixo da reta tangente em \( x=0 \), ou seja: \[ \ln(1+x) \leq x. \]
Ademais, pode ser demonstrado que para \( x > 0 \) também vale a seguinte desigualdade: \[ \ln(1+x) \geq \frac{x}{1+x}. \] Essas desigualdades podem ser resumidas em: \[ \frac{x}{1+x} \leq \ln(1+x) \leq x. \]
Dividindo por \( x \) (para \( x > 0 \)), obtemos: \[ \frac{1}{1+x} \leq \frac{\ln(1+x)}{x} \leq 1. \]
Agora, calculamos os limites dos extremos quando \( x \to 0 \): \[ \lim_{x \to 0} \frac{1}{1+x} = \frac{1}{1+0} = 1 \quad \text{e} \quad \lim_{x \to 0} 1 = 1. \] Pelo teorema do sanduíche, concluímos que: \[ \lim_{x \to 0} \frac{\ln(1+x)}{x} = 1. \]
Portanto, demonstramos por comparação que: \[ \lim_{x \to 0} \frac{\ln(1+x)}{x} = 1. \]
Neste documento demonstramos o seguinte limite notável:
Demonstração pela regra de De L'Hôpital
Observa-se que, definindo \( f(x) = \ln(1+x) \) e \( g(x) = x \), quando \( x \) tende a zero temos \[ f(0) = \ln(1+0) = 0 \quad \text{e} \quad g(0) = 0, \] de forma que o limite assume a forma indeterminada \(\frac{0}{0}\). Essa condição permite aplicar a regra de De L'Hôpital.
Derivamos, então, o numerador e o denominador:
\[ f'(x) = \frac{d}{dx}\ln(1+x) = \frac{1}{1+x}, \quad g'(x) = \frac{d}{dx}x = 1. \]
Aplicando a regra de De L'Hôpital, obtemos: \[ \lim_{x \to 0} \frac{\ln(1+x)}{x} = \lim_{x \to 0} \frac{f'(x)}{g'(x)} = \lim_{x \to 0} \frac{1}{1+x}. \]
Como o limite \(\lim_{x \to 0} \frac{1}{1+x}\) pode ser calculado de imediato, temos: \[ \lim_{x \to 0} \frac{1}{1+x} = \frac{1}{1+0} = 1. \]
Consequentemente, segue que: \[ \lim_{x \to 0} \frac{\ln(1+x)}{x} = 1 \]
Demonstração pela expansão em série de Taylor
Alternativamente, podemos demonstrar o resultado recorrendo à expansão em série de Taylor da função \(\ln(1+x)\) em torno de \( x=0 \):
A série de Taylor de \(\ln(1+x)\) é dada por: \[ \ln(1+x) = x - \frac{x^2}{2} + \frac{x^3}{3} - \cdots, \quad \text{para } |x| < 1. \]
Dividindo por \( x \), obtemos: \[ \frac{\ln(1+x)}{x} = 1 - \frac{x}{2} + \frac{x^2}{3} - \cdots. \]
Fazendo \( x \) tender a zero, todos os termos contendo potências positivas de \( x \) se anulam, restando: \[ \lim_{x \to 0} \frac{\ln(1+x)}{x} = 1. \]
Assim, demonstramos que, por três métodos, temos:
\[ \lim_{x \to 0} \frac{\ln(1+x)}{x} = 1 \]
A primeira demonstração utilizou o critério de comparação, a segunda a regra de De L'Hôpital, enquanto a terceira foi baseada na expansão em série de Taylor.

