A reta é um conceito primitivo da geometria euclidiana, ou seja, não definível em termos mais elementares, mas assumido como ente fundamental. Ela é intuitivamente descrita como o conjunto infinito de pontos dispostos segundo uma direção constante, estendendo-se indefinidamente em ambas as direções. Em um sistema de coordenadas cartesianas, uma reta é representável mediante uma equação linear e caracterizada por um coeficiente angular que determina sua inclinação em relação ao eixo das abscissas.
Índice
- Como encontrar a equação da reta que passa por dois pontos
- Como encontrar a equação explícita da reta
- Como encontrar a equação implícita da reta
- Significado geométrico do coeficiente angular
- Como encontrar a equação paramétrica da reta
- Como encontrar a reta perpendicular a uma reta dada
- Exercícios resolvidos sobre a reta
Como encontrar a equação da reta que passa por dois pontos
Suponhamos que conhecemos dois pontos distintos do plano cartesiano: \( P_1(x_1, y_1) \) e \( P_2(x_2, y_2) \).
A equação dos pontos pertencentes à reta que passa por \( P_1 \) e \( P_2 \) é dada pela seguinte fórmula:
\[ \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1}. \]
Com efeito, basta observar que os triângulos \( \triangle P_1P'P \) e \( \triangle P_1P'_2P_2 \) na figura:
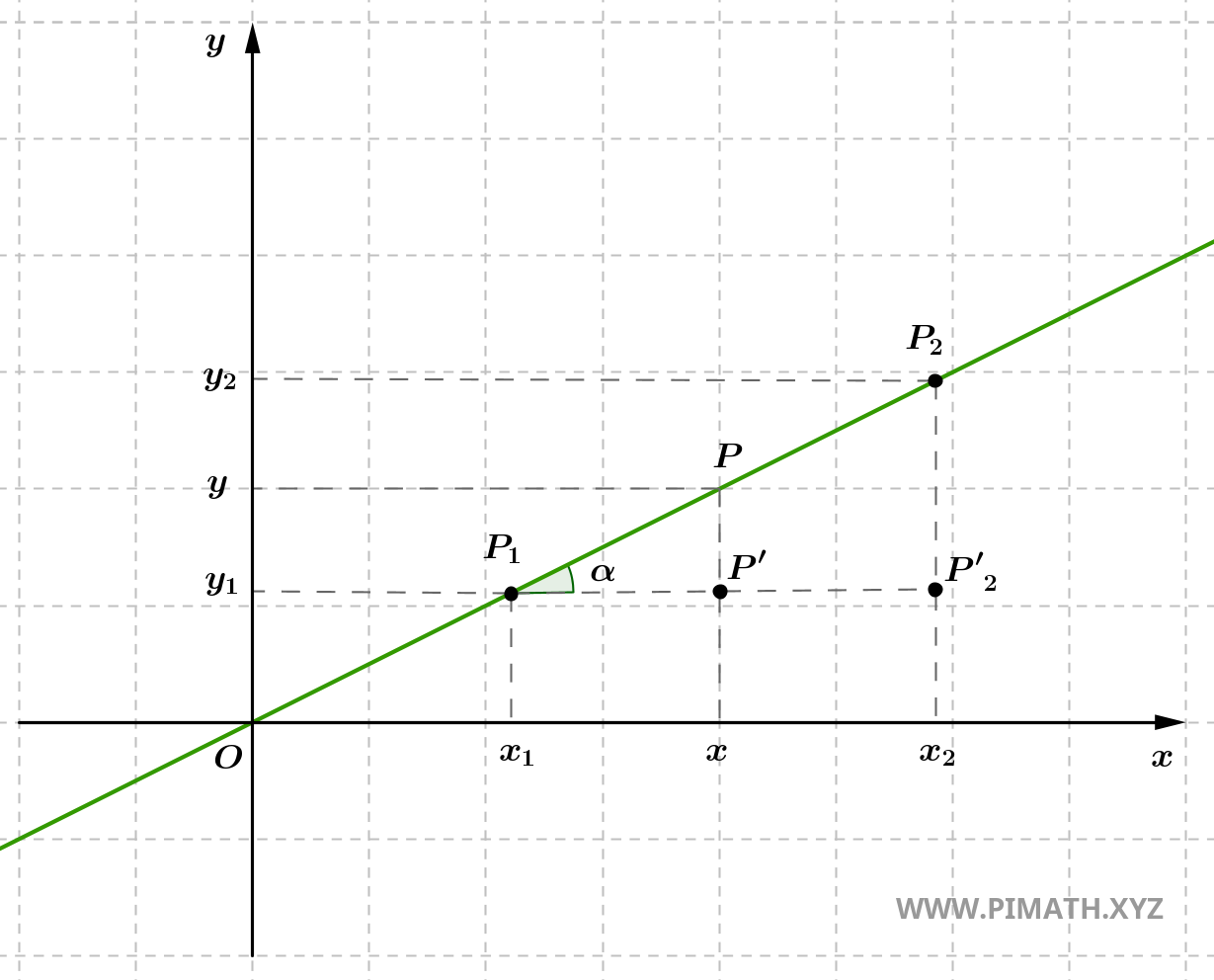
são semelhantes segundo o primeiro critério de semelhança, o qual afirma que dois triângulos são semelhantes se têm dois ângulos respectivamente congruentes. Neste caso, ambos os triângulos apresentam um ângulo reto e um ângulo agudo congruente, determinado pela inclinação da reta em relação ao eixo x. Disso decorre a proporcionalidade entre os lados correspondentes.
\[ \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1} \]
Resolvendo em relação a \( y \), obtém-se a forma explícita da equação da reta:
\[ y - y_1 = \frac{y_2 - y_1}{x_2 - x_1}(x - x_1) \]
O ângulo agudo comum aos dois triângulos, indicado frequentemente com \( \alpha \), representa o ângulo de inclinação da reta em relação ao eixo x. Este ângulo tem um papel fundamental na geometria da reta, pois sua tangente fornece o declive da reta, ou seja: \[ m = \tan \alpha = \frac{y_2 - y_1}{x_2 - x_1}. \] Esta relação permite interpretar o declive como uma medida da inclinação angular da reta no plano cartesiano.
Como encontrar a equação explícita da reta
A equação da reta que passa por dois pontos distintos \( P_1(x_1, y_1) \) e \( P_2(x_2, y_2) \) pode ser escrita em forma explícita utilizando a chamada forma ponto-declive:
\[ y = y_1 + m(x - x_1) \]
onde
\[ m = \displaystyle \frac{y_2 - y_1}{x_2 - x_1} \]
é o coeficiente angular da reta. Esta expressão permite calcular o valor de \( y \) correspondente a cada valor atribuído de \( x \), partindo de um ponto conhecido na reta e do seu declive.
A partir desta forma, é possível obter a forma explícita canónica da equação da reta, que é:
\[ y = mx + b \]
Nesta equação:
- \( m \) é o coeficiente angular, que representa o declive da reta;
- \( b \) é a ordenada na origem, ou seja, o valor de \( y \) no ponto onde a reta interseta o eixo das ordenadas (isto é, quando \( x = 0 \)).
Esta forma é particularmente útil porque torna imediatamente evidentes tanto a direção da reta (através de \( m \)) quanto o seu ponto de interseção com o eixo y (através de \( b \)). Se se conhecem \( m \) e \( b \), é possível traçar a reta sem necessidade de outros pontos.
Para passar da forma ponto-declive para a canónica, basta desenvolver os cálculos e isolar \( y \). Por exemplo:
\[ y = y_1 + m(x - x_1) = mx + (y_1 - mx_1) \]
Do qual se obtém diretamente:
\[ y = mx + b \quad \text{com} \quad b = y_1 - mx_1 \]
Como encontrar a equação implícita da reta
Partamos da forma ponto-declive da equação da reta, que passa por dois pontos \( (x_1, y_1) \) e \( (x_2, y_2) \):
\[ y - y_1 = \frac{y_2 - y_1}{x_2 - x_1} (x - x_1) \]
Multiplicamos ambos os membros por \( x_2 - x_1 \neq 0 \):
\[ (x_2 - x_1)(y - y_1) = (y_2 - y_1)(x - x_1) \]
Desenvolvemos ambos os membros:
\[ (x_2 - x_1)y - (x_2 - x_1)y_1 = (y_2 - y_1)x - (y_2 - y_1)x_1 \]
Passamos todos os termos para o primeiro membro:
\[ (x_2 - x_1)y - (y_2 - y_1)x + \left( (y_2 - y_1)x_1 - (x_2 - x_1)y_1 \right) = 0 \]
Esta é a forma implícita da equação da reta. Se definirmos os coeficientes como:
\[ \begin{cases} a = -(y_2 - y_1) \\ b = x_2 - x_1 \\ c = (y_2 - y_1)x_1 - (x_2 - x_1)y_1 \end{cases} \]
a equação assume a forma geral:
\[ ax + by + c = 0 \]
Alternativamente, se introduzirmos o declive \( m = \displaystyle \frac{y_2 - y_1}{x_2 - x_1} \), podemos partir da forma explícita da reta:
\[ y = m(x - x_1) + y_1 \]
Levamos tudo para o primeiro membro para obter a forma implícita:
\[ y - m x + (m x_1 - y_1) = 0 \]
Portanto, a forma implícita com declive \( m \) é:
\[ a = -m, \quad b = 1, \quad c = m x_1 - y_1 \]
e a forma geral:
\[ ax + by + c = 0 \]
A forma implícita é útil quando se querem estudar propriedades geométricas da reta ou verificar a pertença de um ponto sem ter de resolver para \( y \).
Significado geométrico do coeficiente angular
No contexto desta equação, o termo:
\[ m = \frac{y_2 - y_1}{x_2 - x_1} \]
representa o declive da reta, ou seja, o coeficiente angular. O declive é uma medida da inclinação da reta em relação ao eixo das abscissas (o eixo x). Se o declive é positivo, a reta é crescente (sobe da esquerda para a direita); se é negativo, a reta é decrescente (desce da esquerda para a direita).
Por outras palavras, o declive descreve a velocidade com que a reta cresce ou decresce em relação ao eixo das abscissas x. O declive é um parâmetro crucial para determinar a orientação da reta no plano cartesiano. Dependendo do valor do declive, podemos fazer as seguintes observações:
- Se \( m > 0 \), a reta é crescente, ou seja, sobe da esquerda para a direita. Isto significa que para cada incremento em \( x \), também \( y \) aumenta. A reta forma um ângulo agudo com o eixo x.
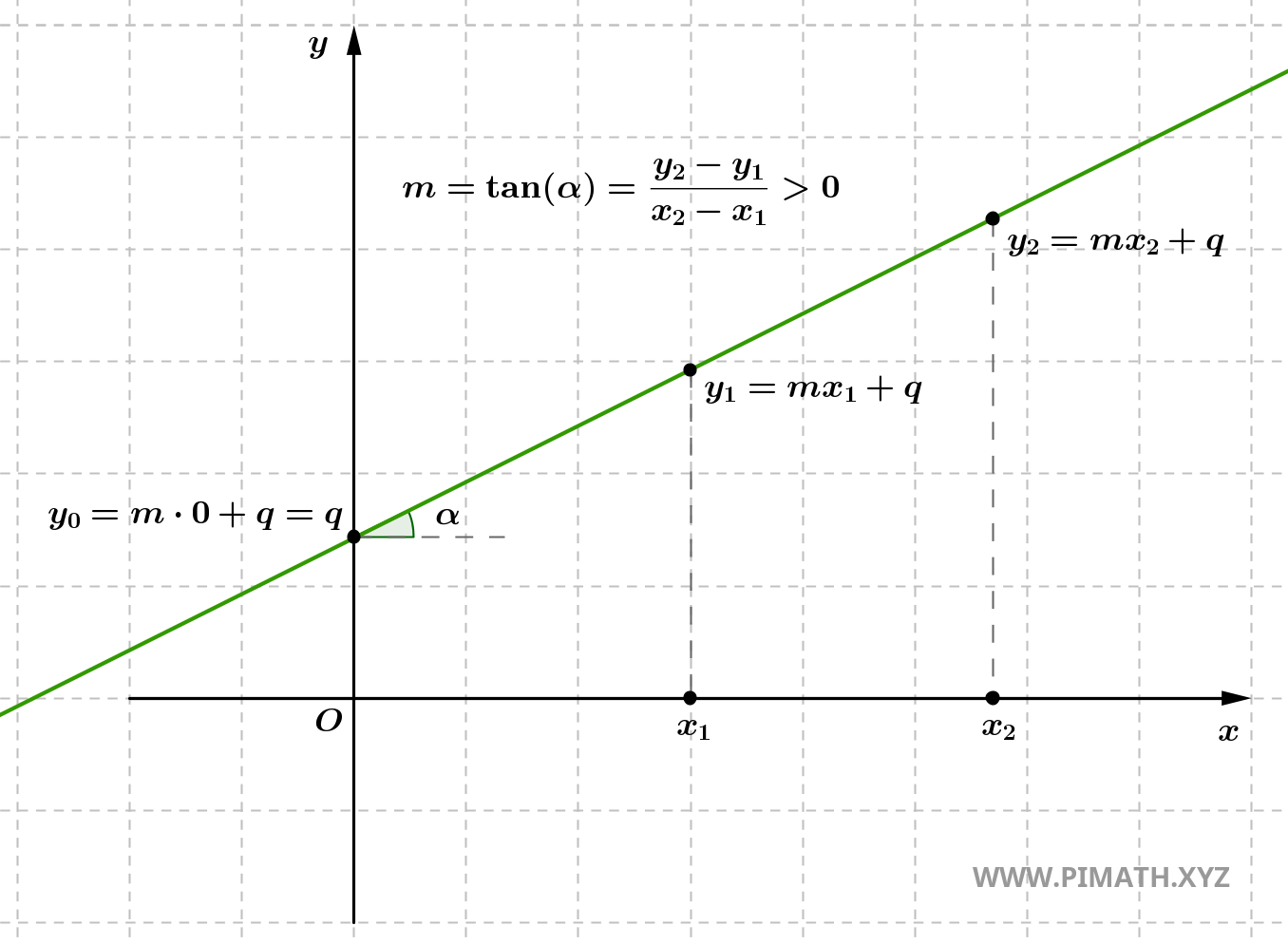
- Se \( m < 0 \), a reta é decrescente, ou seja, desce da esquerda para a direita. Neste caso, para cada incremento em \( x \), o valor de \( y \) diminui. A reta forma um ângulo obtuso com o eixo x.
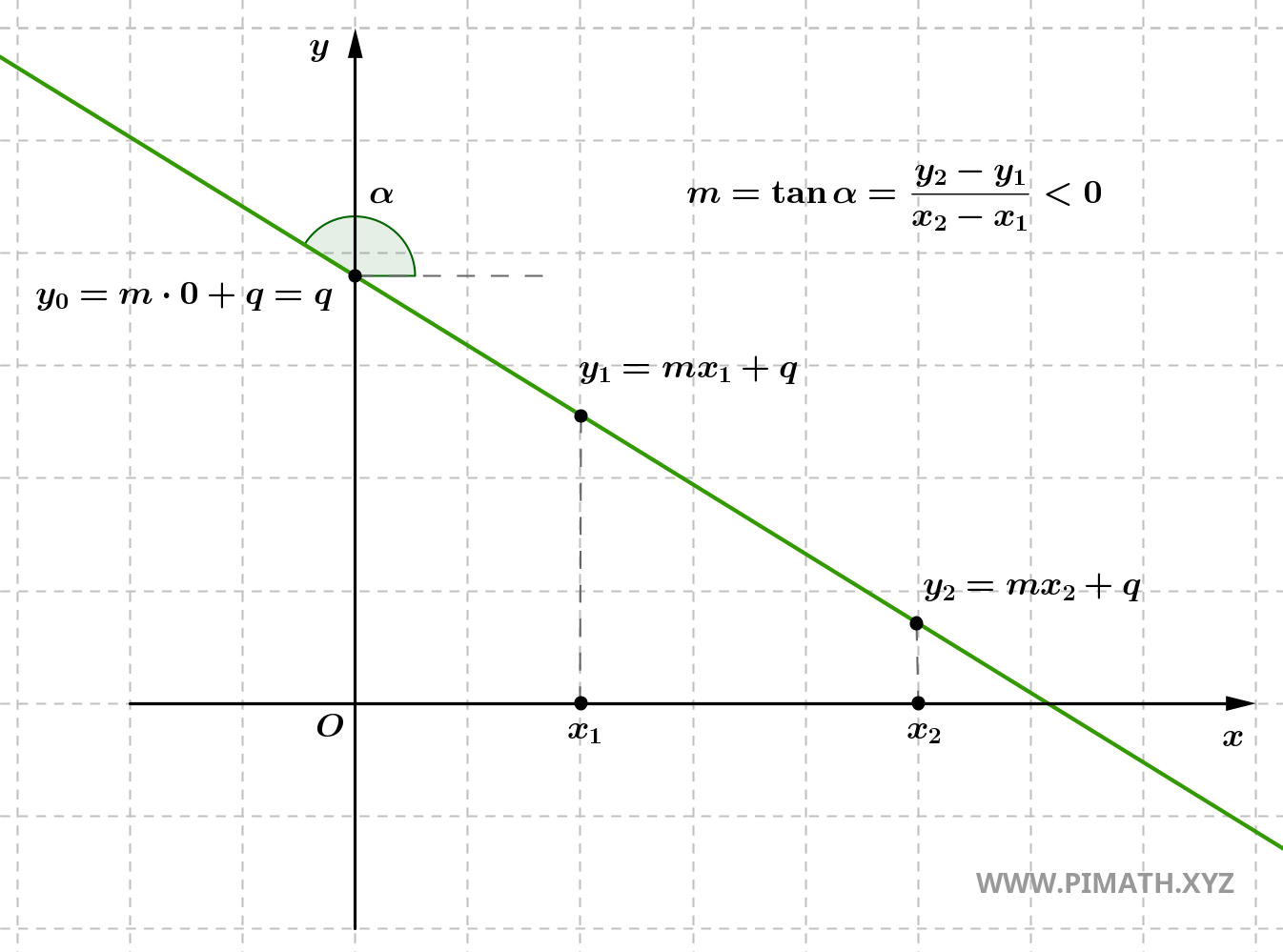
- Se \( y_2 = y_1 \), o declive é nulo, o que implica que a reta é horizontal. Neste caso, não existe mudança vertical (a diferença entre as ordenadas \( y_2 - y_1 \) é zero). A reta é paralela ao eixo x e não tem inclinação vertical.
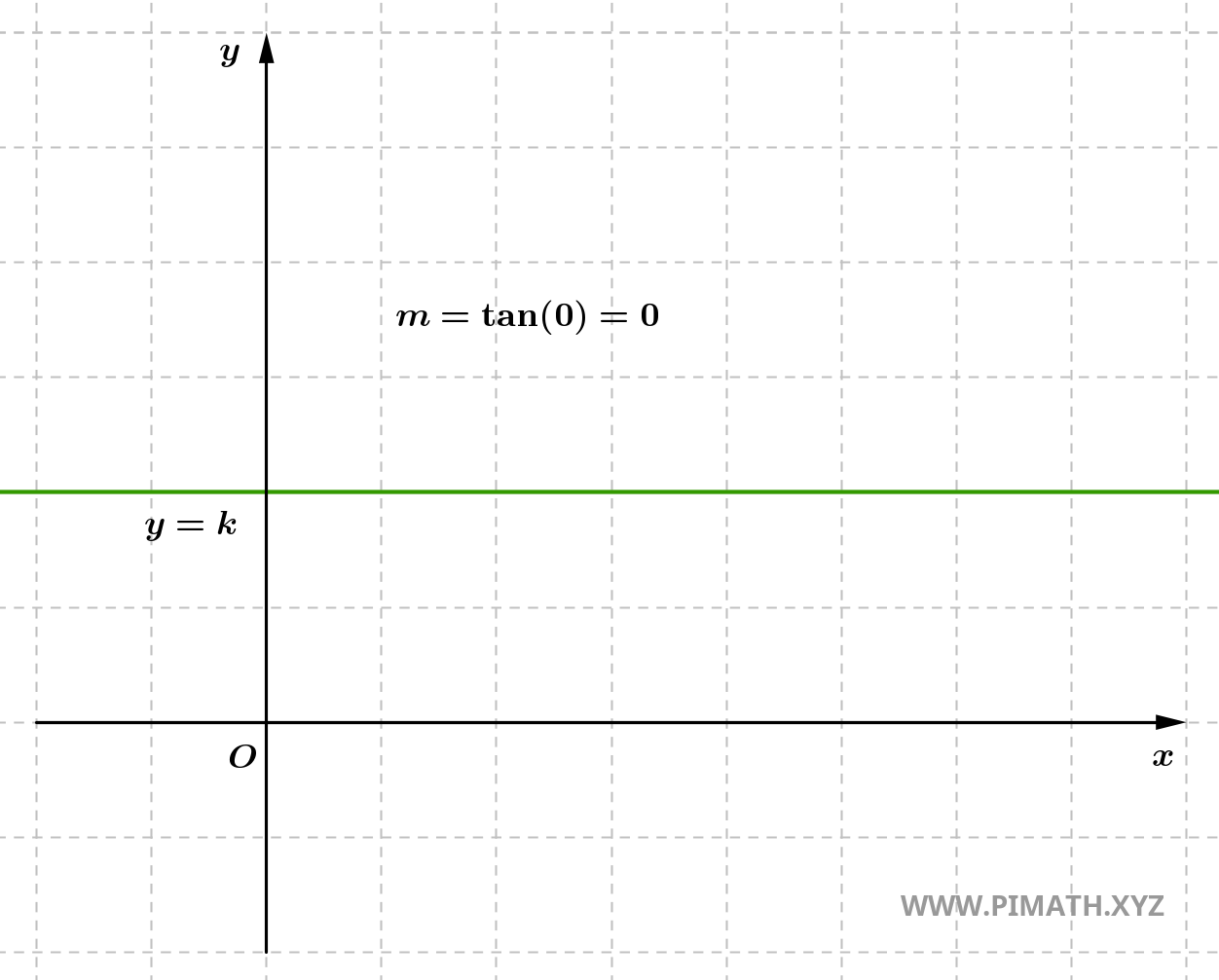
- Se \( x_2 = x_1 \), o declive é indefinido, o que implica que a reta é vertical. Neste caso, não existe mudança horizontal (a diferença entre as abscissas \( x_2 - x_1 \) é zero), portanto não se pode definir um declive numérico. A reta é paralela ao eixo y e não tem inclinação horizontal.
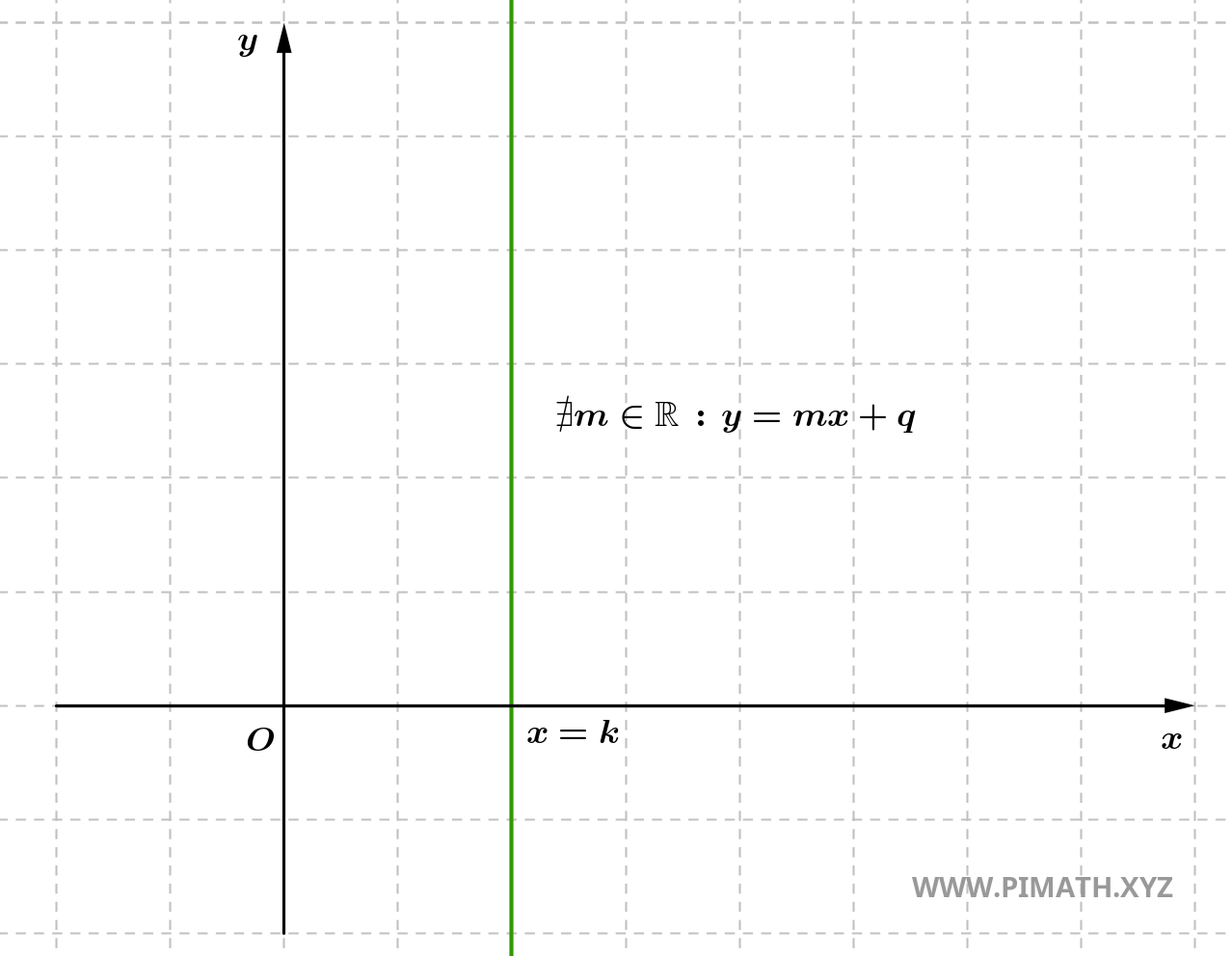
Em geral, o declive \( m \) oferece-nos informação importante sobre o comportamento da reta. Se a reta é crescente, o valor de \( y \) aumenta ao aumentar \( x \); se é decrescente, o valor de \( y \) diminui ao aumentar \( x \); se a reta é vertical, significa que \( y \) não depende de \( x \) e a reta não tem inclinação horizontal.
Como encontrar a equação paramétrica da reta
A reta que passa pelos pontos \( P_1(x_1, y_1) \) e \( P_2(x_2, y_2) \) pode ser descrita também em forma paramétrica. Nesta representação, as coordenadas \( x \) e \( y \) de um ponto na reta são expressas em função de um parâmetro real \( t \), que varia ao longo da reta.
A equação paramétrica da reta é dada por:
\[ \begin{cases} x = x_1 + (x_2 - x_1)t \\ y = y_1 + (y_2 - y_1)t \end{cases} \]
Aqui, \( t \) é o parâmetro que pode assumir qualquer valor real. Quando \( t \) varia, o ponto \( (x, y) \) deslocar-se-á ao longo da reta que liga os dois pontos \( P_1 \) e \( P_2 \).
A forma paramétrica representa portanto uma família de pontos na reta, na qual o parâmetro \( t \) define univocamente cada ponto da reta. Quando \( t = 0 \), obtém-se o ponto \( P_1(x_1, y_1) \); quando \( t = 1 \), obtém-se o ponto \( P_2(x_2, y_2) \). Os valores de \( t \) entre 0 e 1 descrevem os pontos da reta entre \( P_1 \) e \( P_2 \), enquanto os valores de \( t \) superiores a 1 ou inferiores a 0 estendem a reta para além destes pontos.
A fórmula paramétrica baseia-se no conceito de vetor diretor, que é o vetor que liga \( P_1 \) e \( P_2 \). Com efeito, a diferença \( (x_2 - x_1, y_2 - y_1) \) é o vetor diretor da reta, e o parâmetro \( t \) é o fator de escala que permite deslocar-se ao longo da reta.
A forma paramétrica é particularmente útil em vários âmbitos da geometria analítica, como no estudo das curvas em geral.
Como encontrar a reta perpendicular a uma reta dada
Quando duas retas são perpendiculares, o seu declive está ligado por uma relação bem precisa. Se uma reta tem declive \( m \), o declive da reta perpendicular a ela é dado por:
\[ m_\perp = -\frac{1}{m}. \]
Esta fórmula expressa o facto de que o produto dos declives de duas retas perpendiculares é igual a \(-1\). A razão desta relação pode ser vista no facto de que os ângulos formados pelas duas retas devem ser de 90° (um ângulo reto), e portanto a tangente do ângulo entre as retas deve satisfazer esta condição.
Para encontrar a equação da reta perpendicular que passa por um ponto \( (x_1, y_1) \), podemos usar a forma ponto-declive. O declive da reta perpendicular é \( -\displaystyle \frac{1}{m} \), portanto a equação da reta perpendicular será:
\[ y - y_1 = -\frac{1}{m} (x - x_1). \]
Nesta equação, \( (x_1, y_1) \) é o ponto através do qual passa a reta perpendicular, enquanto \( m \) é o declive da reta original. A fórmula descreve uma reta que tem o declive oposto e inverso em relação à reta original.
Se a reta original é representada pela equação \( y = mx + b \), a reta perpendicular terá o declive \( m_\perp = -\displaystyle \frac{1}{m} \) e será escrita na forma \( y - y_1 = -\displaystyle \frac{1}{m} (x - x_1) \), onde \( (x_1, y_1) \) é o ponto de interseção entre a reta original e a reta perpendicular.
Esta propriedade das retas perpendiculares é fundamental em muitos âmbitos da geometria, da trigonometria e da física, em particular quando se estudam ângulos e trajetórias perpendiculares entre si.
Exercícios resolvidos sobre a reta
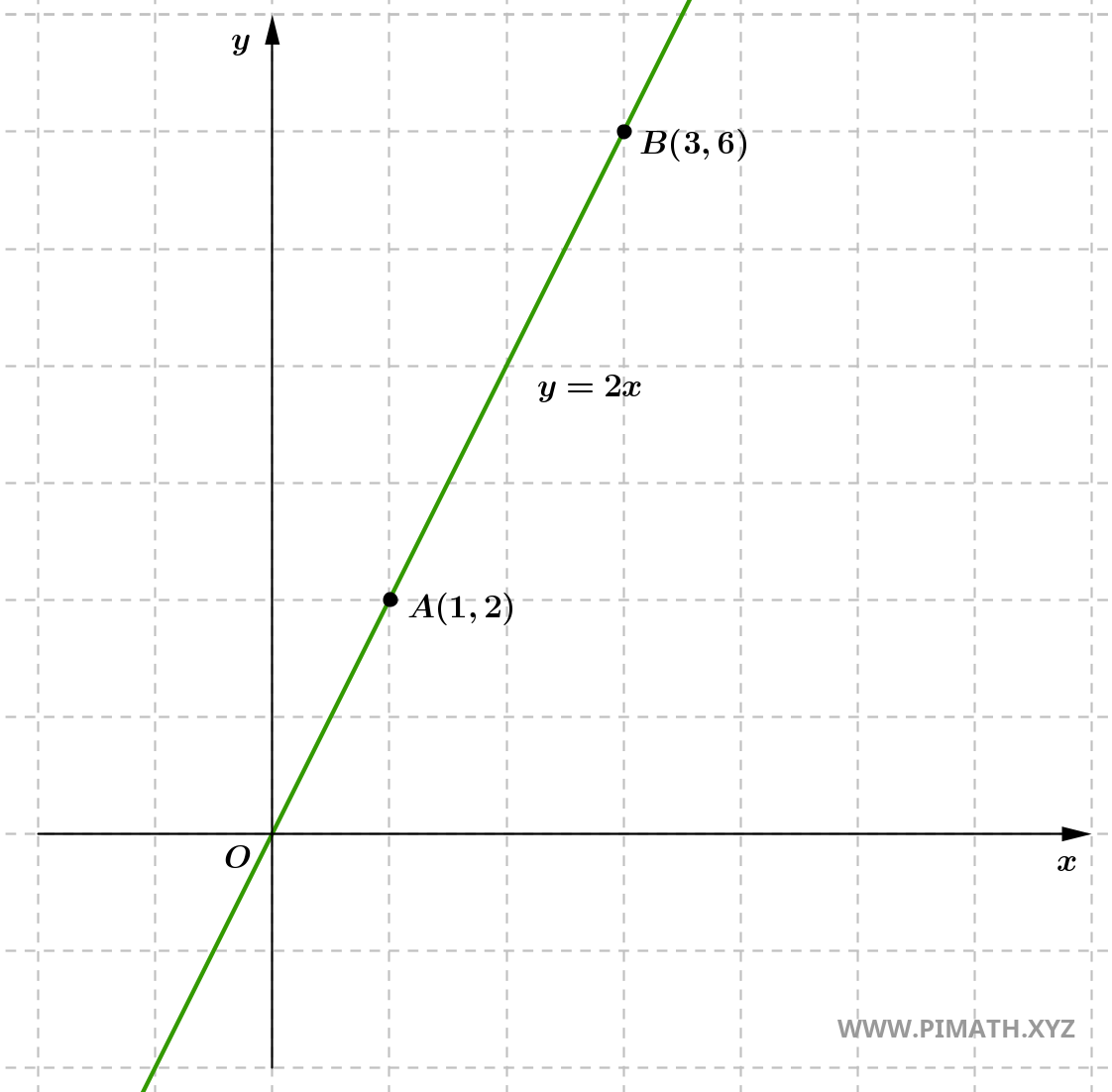
Exercício 1: Determina a equação explícita da reta que passa por \( A(1, 2) \) e \( B(3, 6) \).
Solução. Calculamos o coeficiente angular da reta:
\[ m = \frac{6 - 2}{3 - 1} = \frac{4}{2} = 2. \]
- Utilizamos a equação ponto-declive para determinar a equação da reta que passa por \( A(1, 2) \) e coeficiente angular \( m = 2 \): \[ y - 2 = 2(x - 1). \]
- Desenvolvendo a equação: \[ y - 2 = 2x - 2. \]
- Simplificando: \[ y = 2x - 2 + 2 = 2x. \]
Portanto, a equação da reta que passa pelos pontos \( A(1, 2) \) e \( B(3, 6) \) é \[ y = 2x. \]
Verificação: Podemos verificar que ambos os pontos satisfazem esta equação:
- Para \( A(1, 2) \): \[ 2 = 2 \cdot 1 = 2 \]
- Para \( B(3, 6) \): \[ 6 = 2 \cdot 3 = 6 \]
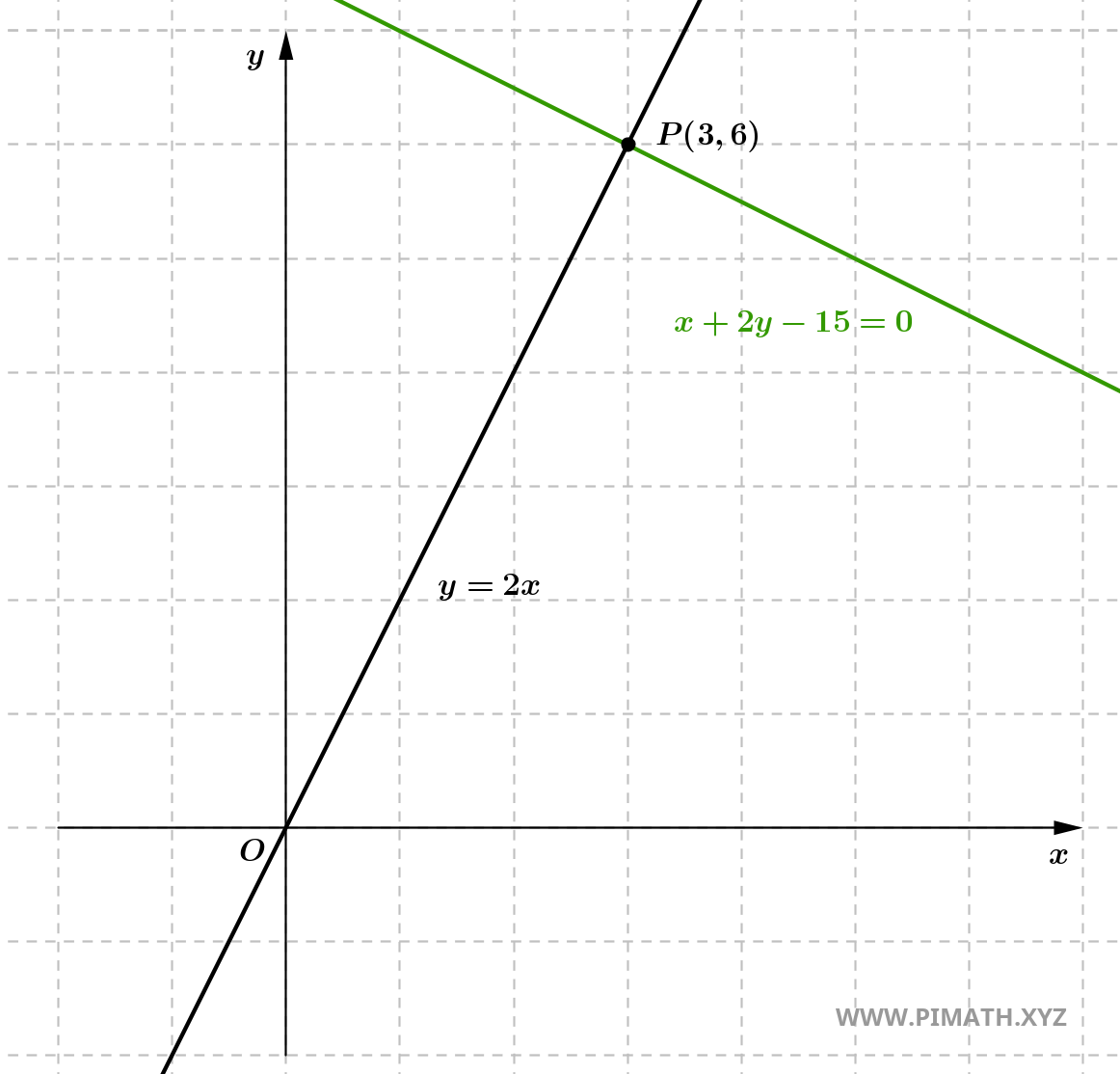
Exercício 2: Determina a equação da reta perpendicular à reta \( y = 2x \) e que passa pelo ponto \( P(3, 6) \).
Solução. A reta dada tem coeficiente angular \( m = 2 \). O coeficiente angular da reta perpendicular será:
\[ m_{\perp} = -\frac{1}{2}. \]
- Utilizamos a equação ponto-declive para determinar a equação da reta que passa por \( P(3, 6) \) e tem coeficiente angular \( m_{\perp} = -\frac{1}{2} \): \[ y - 6 = -\frac{1}{2}(x - 3). \]
- Desenvolvemos a equação: \[ y - 6 = -\frac{1}{2}x + \frac{3}{2}. \]
- Passamos o termo independente para a direita: \[ y = -\frac{1}{2}x + \frac{3}{2} + 6 = -\frac{1}{2}x + \frac{15}{2}. \]
Portanto, a equação da reta procurada é: \[ y = -\frac{1}{2}x + \frac{15}{2}. \]
Forma implícita: Multiplicamos ambos os membros por 2:
\[ 2y = -x + 15 \quad \Rightarrow \quad x + 2y - 15 = 0. \]
Verificação: Substituindo as coordenadas de \( P(3, 6) \) na equação explícita:
- \[ y = -\frac{1}{2}x + \frac{15}{2} \quad \Rightarrow \quad 6 = -\frac{1}{2} \cdot 3 + \frac{15}{2} = -\frac{3}{2} + \frac{15}{2} = \frac{12}{2} = 6. \]
O ponto pertence à reta, portanto a solução é correta.
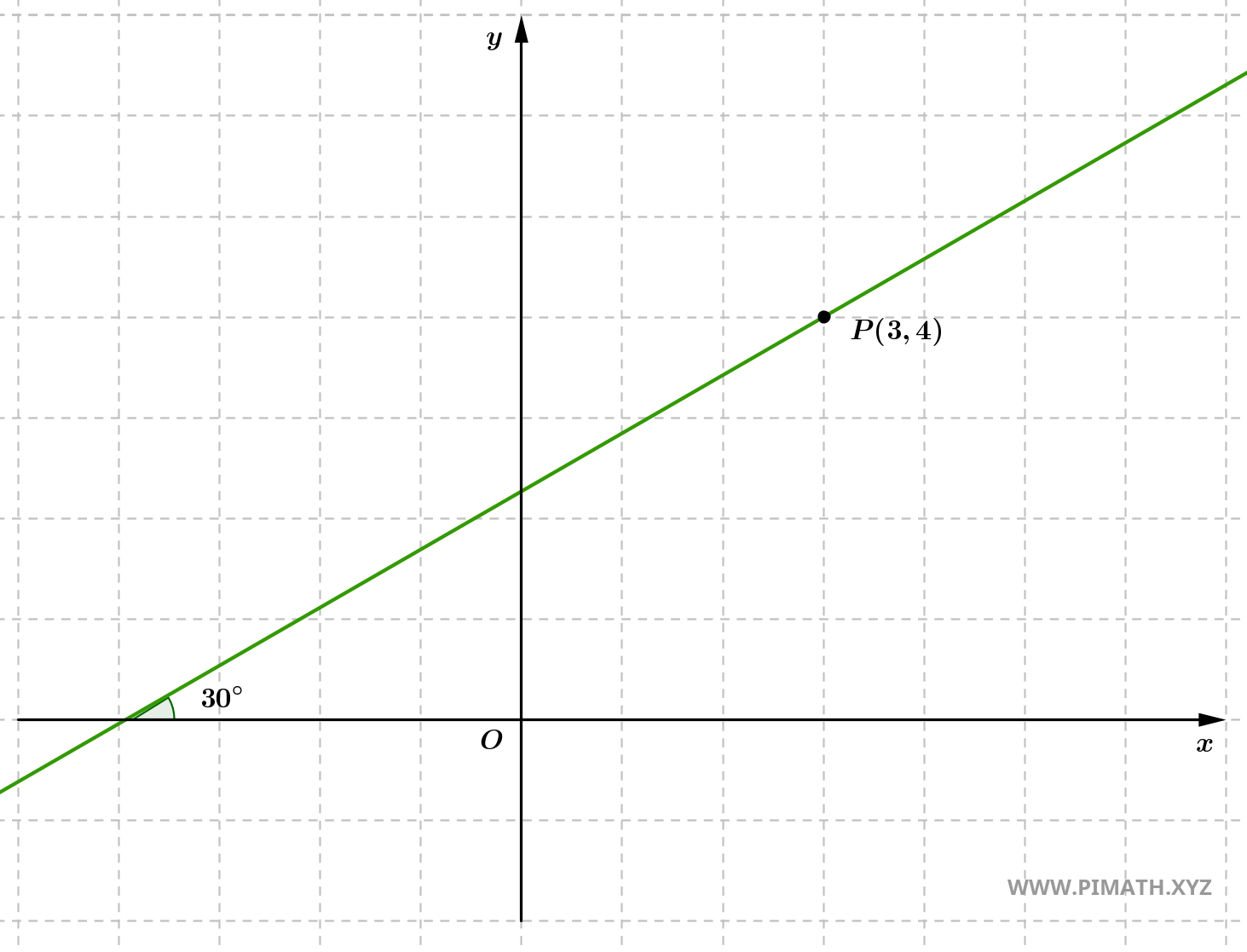
Exercício 3: Determina a equação da reta que passa pelo ponto \( P(3, 4) \) e que forma um ângulo de \( 30^\circ \) com o eixo das abscissas.
Solução. O ângulo que uma reta forma com o eixo das abscissas está ligado ao coeficiente angular através da tangente:
\[ m = \tan(30^\circ) = \tan\left( \frac{\pi}{6} \right) = \frac{1}{\sqrt{3}}. \]
- Utilizamos a equação ponto-declive com o ponto \( P(3, 4) \) e coeficiente angular \( m = \frac{1}{\sqrt{3}} \): \[ y - 4 = \frac{1}{\sqrt{3}}(x - 3). \]
- Desenvolvendo a equação: \[ y - 4 = \frac{1}{\sqrt{3}}x - \frac{3}{\sqrt{3}} = \frac{1}{\sqrt{3}}x - \sqrt{3}. \]
- Adicionamos 4 a ambos os membros: \[ y = \frac{1}{\sqrt{3}}x - \sqrt{3} + 4. \]
- Simplificando o termo independente: \[ y = \frac{1}{\sqrt{3}}x + (4 - \sqrt{3}). \]
Portanto, a equação da reta procurada é: \[ y = \frac{1}{\sqrt{3}}x + (4 - \sqrt{3}). \]
Verificação: Substituindo \( x = 3 \), obtemos: \[ y = \frac{1}{\sqrt{3}} \cdot 3 + (4 - \sqrt{3}) = \sqrt{3} + 4 - \sqrt{3} = 4. \]
- O ponto \( P(3, 4) \) pertence à reta, portanto a solução é correta.
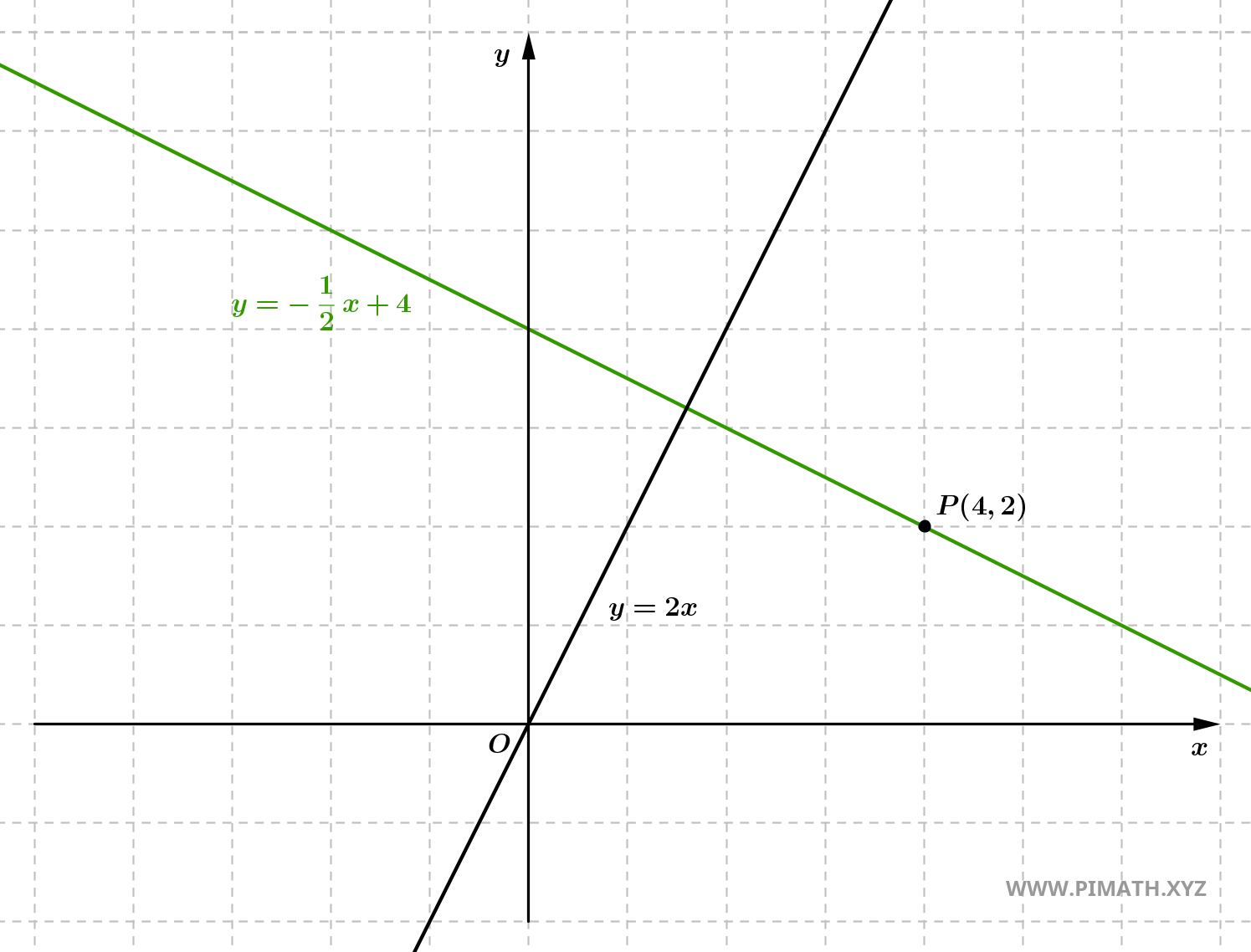
Exercício 4: Determina a equação da reta perpendicular à reta \( y = 2x \) e que passa pelo ponto \( P(4, 2) \).
Solução. A reta dada tem coeficiente angular \( m = 2 \). O coeficiente angular da reta perpendicular será:
\[ m_{\perp} = -\frac{1}{2}. \]
- Utilizamos a equação ponto-declive para determinar a equação da reta que passa por \( P(4, 2) \) e tem coeficiente angular \( m_{\perp} = -\frac{1}{2} \): \[ y - 2 = -\frac{1}{2}(x - 4). \]
- Desenvolvemos a equação: \[ y - 2 = -\frac{1}{2}x + 2. \]
- Passamos o termo independente para a direita: \[ y = -\frac{1}{2}x + 2 + 2 = -\frac{1}{2}x + 4. \]
Portanto, a equação da reta procurada é: \[ y = -\frac{1}{2}x + 4. \]
Forma implícita: Multiplicamos ambos os membros por 2:
\[ 2y = -x + 8 \quad \Rightarrow \quad x + 2y - 8 = 0. \]
Verificação: Substituindo as coordenadas de \( P(4, 2) \) na equação explícita:
- \[ y = -\frac{1}{2}x + 4 \quad \Rightarrow \quad 2 = -\frac{1}{2} \cdot 4 + 4 = -2 + 4 = 2. \]
O ponto pertence à reta, portanto a solução é correta.
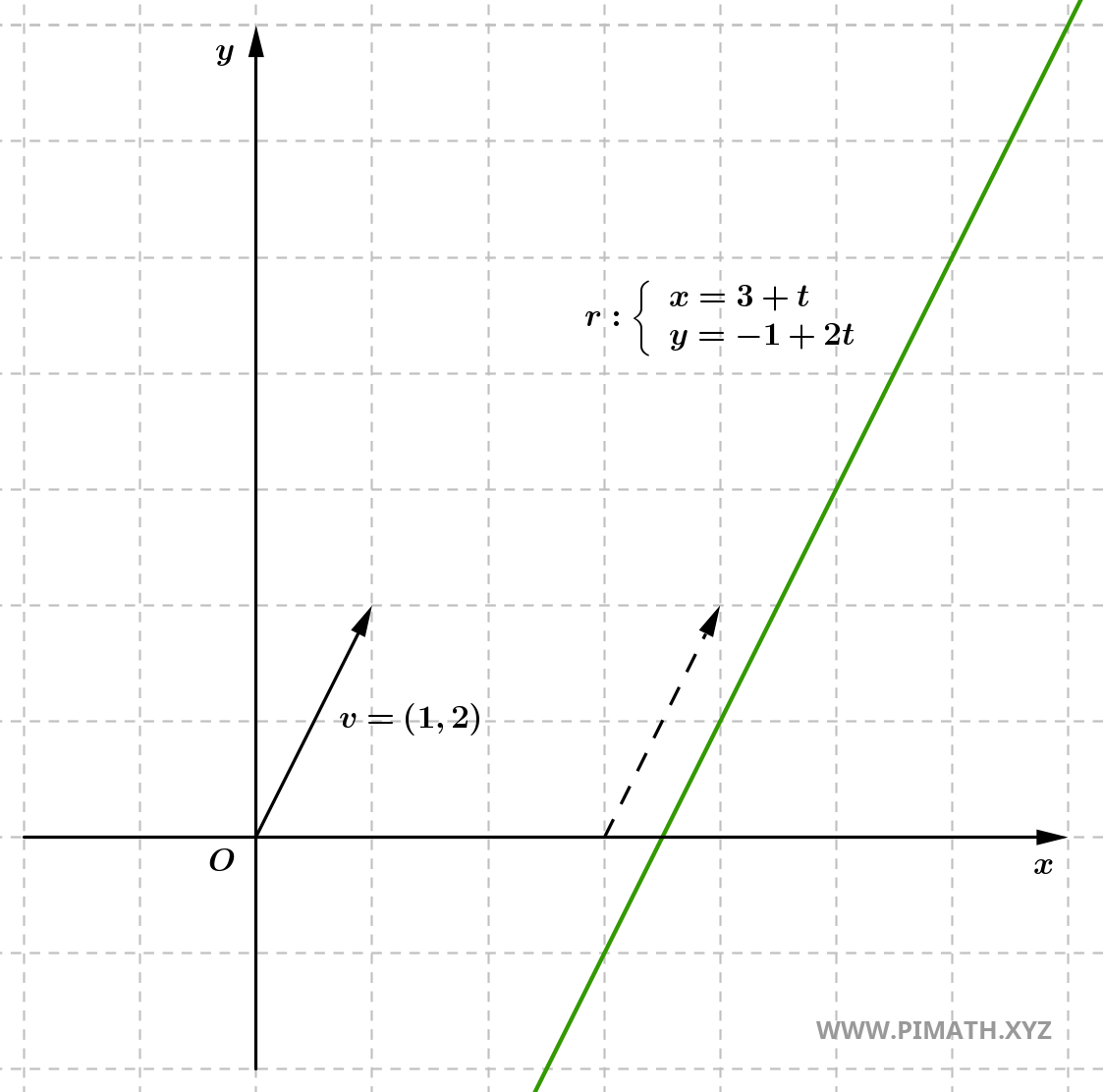
Exercício 5: Escreve a equação paramétrica da reta que passa por \( A(3, -1) \) e \( B(4, 1) \). Em seguida, escreve a equação paramétrica em forma cartesiana.
Solução. Calculamos o vetor diretor \( \boldsymbol{v} = (x_2 - x_1, y_2 - y_1) \), que representa a direção da reta:
\[ \boldsymbol{v} = (4 - 3,\ 1 - (-1)) = (1,\ 2). \]
As equações paramétricas da reta são:
\[ r: \begin{cases} x = 3 + t \\ y = -1 + 2t \end{cases} \quad \text{com} \quad t \in \mathbb{R}. \]
Passemos agora à forma cartesiana. Obtemos \( t \) da primeira equação:
\[ x = 3 + t \quad \Rightarrow \quad t = x - 3. \]
Substituindo na segunda:
\[ y = -1 + 2(x - 3) = -1 + 2x - 6 = 2x - 7. \]
Portanto, a forma explícita é:
\[ y = 2x - 7. \]
Finalmente, passando tudo para o primeiro membro obtemos a forma implícita:
\[ 2x - y - 7 = 0. \]