A parábola é o lugar geométrico dos pontos do plano para os quais a distância a um ponto fixo (foco) é igual à distância a uma reta fixa (diretriz). Possui um eixo de simetria que passa pelo foco e é perpendicular à diretriz. É uma curva aberta e simétrica em relação ao seu próprio eixo, com numerosas aplicações em física e geometria.
Índice
- Equação Canónica da Parábola
- Equação Canónica de uma Parábola com Eixo Vertical ou Horizontal
- Parábola Transladada no Plano
- Vértice, Foco, Diretriz e Eixos de Simetria
- Equação da Parábola Conhecidos o Vértice e um Ponto
- Exercícios Resolvidos sobre a Parábola
Equação Canónica da Parábola
Uma parábola é o lugar geométrico dos pontos \( P(x, y) \) do plano que têm a mesma distância a um ponto fixo, chamado foco, e a uma reta fixa, chamada diretriz.
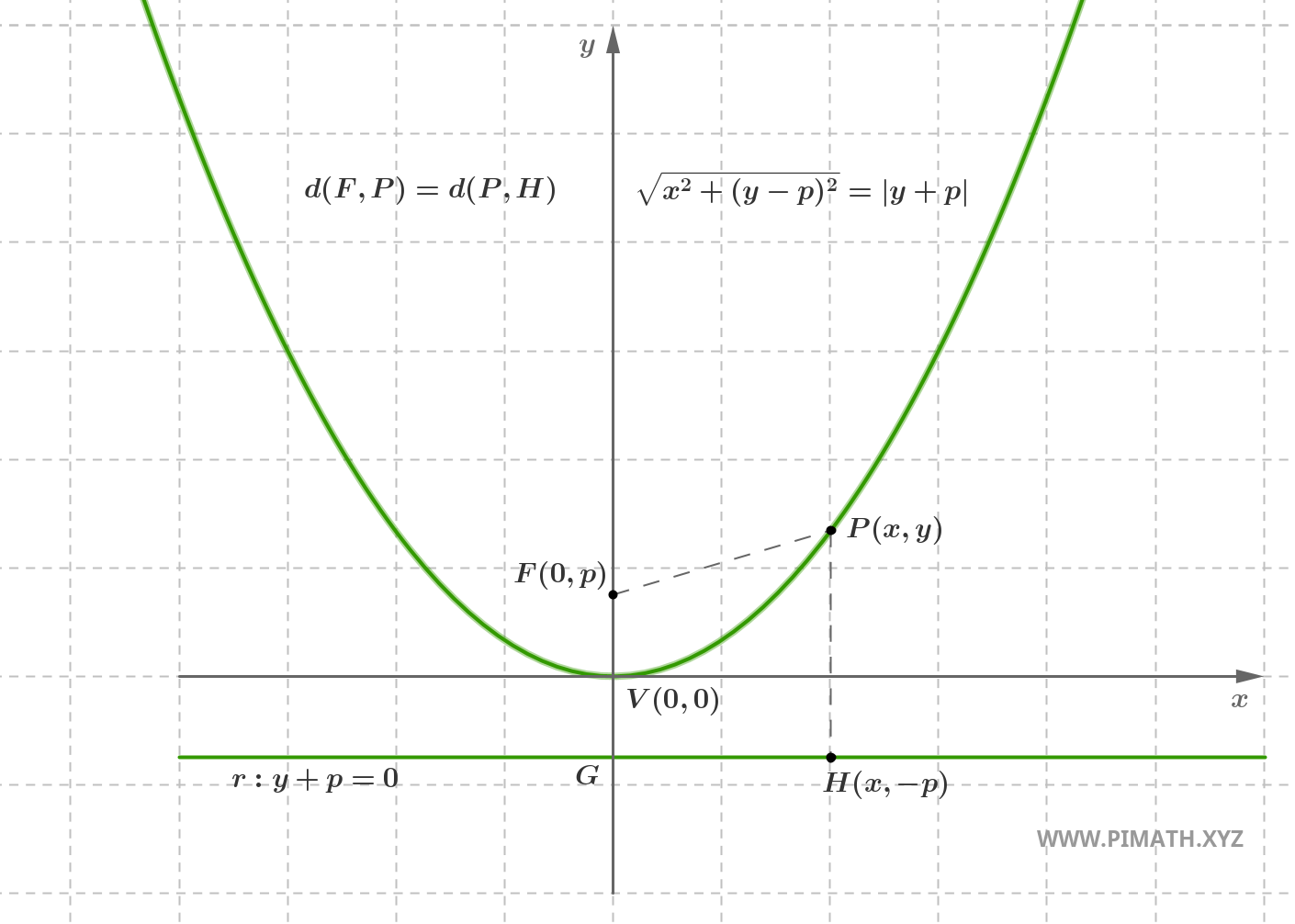
Seja \( F(0, p) \) com \( p > 0 \) o foco e seja \( r \) a diretriz, de equação \( y = -p \). Por definição, os pontos \( P(x, y) \) da parábola satisfazem:
\[ \text{d}(P, F) = \text{d}(P, r) \]
Calculamos a distância entre \( P(x, y) \) e o foco \( F(0, p) \):
\[ \text{d}(P, F) = \sqrt{(x - 0)^2 + (y - p)^2} = \sqrt{x^2 + (y - p)^2} \]
Agora, calculamos a distância entre \( P(x, y) \) e a reta diretriz \( y = -p \):
\[ \text{d}(P, r) = |y - (-p)| = |y + p| \]
Finalmente, impomos a igualdade entre as duas distâncias:
\[ \sqrt{x^2 + (y - p)^2} = |y + p| \]
Observação: uma vez que a parábola se encontra acima da diretriz (dado que o foco está acima da diretriz para \( p > 0 \)), todos os pontos da parábola satisfazem \( y \geq -p \). Portanto \( y + p \geq 0 \) e podemos retirar o valor absoluto:
\[ \sqrt{x^2 + (y - p)^2} = y + p \]
Elevamos ao quadrado ambos os membros:
\[ x^2 + (y - p)^2 = (y + p)^2 \]
Desenvolvemos os quadrados:
\[ x^2 + y^2 - 2py + p^2 = y^2 + 2py + p^2 \]
Simplificamos ambos os lados:
\[ x^2 - 2py = 2py \]
Levamos tudo para o segundo membro:
\[ x^2 = 4py \]
Finalmente, dividimos por \( 4p \):
\[ y = \frac{1}{4p}x^2 \]
Se pomos \( a = \displaystyle \frac{1}{4p} \), obtemos a forma mais compacta:
\[ y = ax^2 \]
que é a equação canónica da parábola com vértice na origem \( V(0, 0) \), foco em \( F(0, p) \) e diretriz \( y = -p \).
Em resumo, a parábola de equação \( y = ax^2 \) tem eixo de simetria vertical, coincidente com o eixo \( y \), e a concavidade voltada para cima se \( a > 0 \), ou para baixo se \( a < 0 \).
Equação Canónica de uma Parábola com Eixo Vertical ou Horizontal
A equação canónica da parábola assume formas diferentes segundo a orientação do eixo de simetria. Distinguimos dois casos fundamentais conforme o eixo seja vertical ou horizontal.
Parábola com Eixo Vertical
Para uma parábola com eixo de simetria vertical, paralelo ao eixo das ordenadas, a equação canónica é \( y = ax^2 \) ou, na forma equivalente, \( x^2 = 4py \). Nesta configuração, o coeficiente \( a = \displaystyle \frac{1}{4p} \) representa o coeficiente diretor, enquanto \( p \) é o parâmetro focal que indica a distância do vértice ao foco.
Os elementos característicos são: o Vértice: \( V(0, 0) \), o Foco \( F\left(0, \displaystyle \frac{1}{4a}\right) \), a Diretriz: \( y = -\displaystyle\frac{1}{4a} \), o Eixo de simetria: \( x = 0 \) (eixo \( y \)) e a Concavidade: para cima se \( a > 0 \), para baixo se \( a < 0 \)
Exemplo: Consideremos a parábola \( y = 2x^2 \). Aqui \( a = 2 \), portanto \( p = \displaystyle \frac{1}{4a} = \displaystyle \frac{1}{8} \). O vértice é \( V(0, 0) \), o foco encontra-se em \( F\left(0, \displaystyle \frac{1}{8}\right) \) e a diretriz tem equação \( y = -\displaystyle \frac{1}{8} \). Uma vez que \( a > 0 \), a parábola apresenta concavidade para cima.
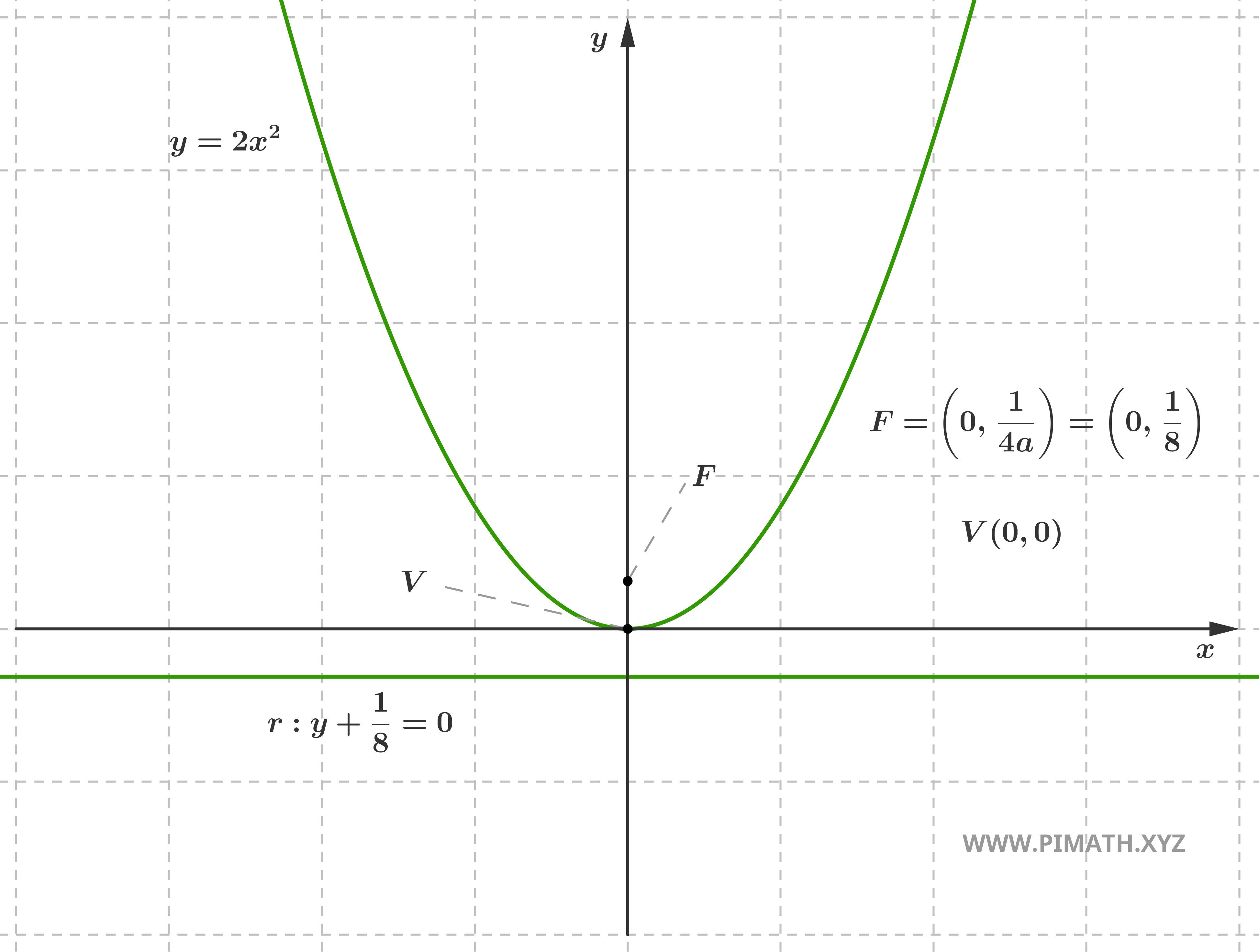
Parábola com Eixo Horizontal
Para uma parábola com eixo de simetria horizontal, paralelo ao eixo das abscissas, a equação canónica torna-se \( x = ay^2 \) (se tomarmos o foco em \( (p, 0) \)), ou, equivalentemente, \( y^2 = 4px \). Também neste caso, \( a = \displaystyle \frac{1}{4p} \) é o coeficiente diretor e \( p \) representa o parâmetro focal.
Elementos característicos: o Vértice: \( V(0, 0) \), o Foco: \( F\left(\displaystyle \frac{1}{4a}, 0\right) \), a Diretriz: \( x = -\displaystyle \frac{1}{4a} \) o Eixo de simetria: \( y = 0 \) (eixo \( x \)), e a Concavidade: para a direita se \( a > 0 \), para a esquerda se \( a < 0 \).
Exemplo: Consideremos a parábola \( x = \displaystyle 2y^2 \). Aqui \( a = 2 \), portanto \( p = \displaystyle \frac{1}{4a} = \frac{1}{8} \). O vértice é \( V(0, 0) \), o foco encontra-se em \( F\left(\displaystyle \frac{1}{8}, 0\right) \) e a diretriz tem equação \( x = -\displaystyle \frac{1}{8} \). Uma vez que \( a > 0 \), a parábola apresenta concavidade para a direita.
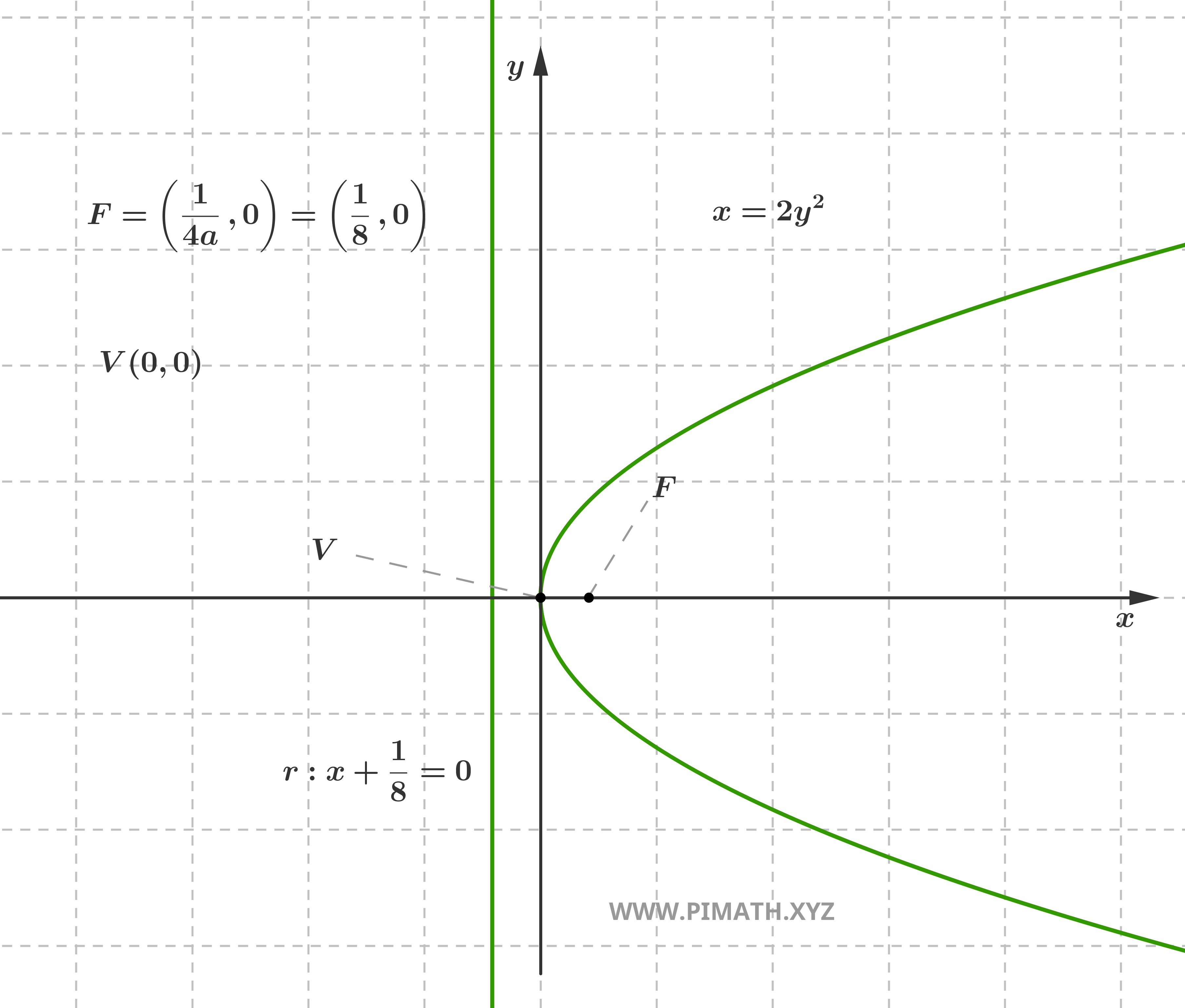
Relação entre os Parâmetros
É fundamental compreender a relação que liga o coeficiente \( a \) ao parâmetro focal \( p \), expressa pela fórmula \( a = \displaystyle \frac{1}{4p} \), que equivale a \( p = \displaystyle \frac{1}{4a} \). Esta relação permite-nos converter facilmente de uma forma para a outra da equação canónica e determinar imediatamente as características geométricas da parábola uma vez conhecido um dos dois parâmetros.
Independentemente da orientação do eixo de simetria, cada ponto \( P(x, y) \) pertencente à parábola respeita sempre a propriedade característica que define geometricamente esta cónica: a distância do ponto ao foco é sempre igual à distância do ponto à diretriz.
Parábola Transladada no Plano
Uma parábola transladada obtém-se operando uma transformação do plano cartesiano (translação). Este tipo de transformação geométrica mantém inalterada a forma da parábola, modificando apenas a sua posição, e representa uma das ferramentas mais importantes para descrever parábolas com vértice em pontos arbitrários do plano.
Transformação de Translação
A translação é uma transformação geométrica que desloca cada ponto do plano de um vetor constante \( \vec{v} = (h, k) \). Se aplicarmos uma translação de vetor \( (h, k) \) à parábola canónica \( y = ax^2 \), obtemos uma nova parábola cujo vértice se desloca da origem para o ponto \( V(h, k) \).
Equação da Parábola Transladada com Eixo Vertical
Partindo da parábola canónica \( y = ax^2 \) com vértice na origem, uma translação de vetor \( (h, k) \) produz a parábola transladada de equação:
\[ y = a(x - h)^2 + k \]
Esta é a forma do vértice da equação parabólica. O parâmetro \( a \) mantém o seu significado originário e determina a abertura e orientação da parábola, enquanto \( h \) e \( k \) representam respetivamente a translação horizontal e vertical do vértice.
Desenvolvendo a expressão \( (x - h)^2 = x^2 - 2hx + h^2 \), obtemos a forma desenvolvida:
\[ y = ax^2 - 2ahx + ah^2 + k \]
Pondo \( b = -2ah \) e \( c = ah^2 + k \), reencontramos a forma geral \( y = ax^2 + bx + c \). Desta relação podemos deduzir que \( h = -\displaystyle \frac{b}{2a} \) e \( k = c - ah^2 = c - \displaystyle \frac{b^2}{4a} \).
Elementos Geométricos da Parábola Transladada
Para uma parábola transladada \( y = a(x - h)^2 + k \), todos os elementos geométricos característicos sofrem a mesma translação aplicada à parábola canónica: o Vértice: \( V(h, k) \), o Eixo de simetria: \( x = h \), o Foco: \( F\left(h, k + \displaystyle \frac{1}{4a}\right) \) e a Diretriz: \( y = k - \displaystyle \frac{1}{4a} \).
A distância entre foco e diretriz permanece invariável e igual a \( 2p = \displaystyle \frac{1}{2|a|} \), assim como todas as propriedades métricas da parábola.
Exemplo de Parábola Transladada
Consideremos a parábola \( y = 2(x - 3)^2 - 5 \). Esta é uma parábola obtida transladando a parábola canónica \( y = 2x^2 \) de \( 3 \) unidades para a direita e \( 5 \) unidades para baixo.
O vértice encontra-se no ponto \( V(3, -5) \), o eixo de simetria tem equação \( x = 3 \). O parâmetro focal é \( p = \displaystyle \frac{1}{4 \cdot 2} = \displaystyle \frac{1}{8} \).
Vértice, Foco, Diretriz e Eixos de Simetria
Os elementos geométricos característicos de uma parábola são o vértice, o foco e a diretriz. Estes três elementos estão ligados entre si e determinam completamente a forma e posição da parábola no plano cartesiano.
O Vértice da Parábola
Definição. O vértice é o ponto da parábola que realiza o extremo absoluto (máximo ou mínimo, depende do sinal de \( a \)) da função quadrática \( f(x) = ax^2 + bx + c \).
As coordenadas do vértice são:
\[ V\left(-\frac{b}{2a}, -\frac{\Delta}{4a}\right) \]
onde \( \Delta = b^2 - 4ac \) é o discriminante.
Demonstração. Transformamos a equação \( y = ax^2 + bx + c \) em forma canónica mediante completamento do quadrado:
\[ y = a\left(x^2 + \frac{b}{a}x\right) + c \]
\[ y = a\left(x^2 + \frac{b}{a}x + \left(\frac{b}{2a}\right)^2 - \left(\frac{b}{2a}\right)^2\right) + c \]
\[ y = a\left(x + \frac{b}{2a}\right)^2 - \frac{b^2}{4a} + c = a\left(x + \frac{b}{2a}\right)^2 - \frac{\Delta}{4a} \]
Da forma canónica \( y = a(x - h)^2 + k \) lê-se o vértice \( V(h, k) \), portanto
\[ V\left(-\frac{b}{2a}, -\frac{\Delta}{4a}\right) \]
Propriedades do vértice:
- Encontra-se sobre o eixo de simetria \( x = -\displaystyle \frac{b}{2a} \)
- É ponto de mínimo se \( a > 0 \), de máximo se \( a < 0 \)
- É o ponto da parábola mais próximo da diretriz
O Foco da Parábola
Definição. O foco é o ponto fixo tal que cada ponto da parábola é equidistante do foco e da diretriz.
Coordenadas do foco:
\[ F\left(-\frac{b}{2a}, -\frac{\Delta}{4a} + \frac{1}{4a}\right) \]
Demonstração. Na forma canónica transladada \( Y = aX^2 \) (com \( X = x + \displaystyle \frac{b}{2a} \), \( Y = y + \displaystyle \frac{\Delta}{4a} \)), o foco encontra-se em \( \left(0, \displaystyle \frac{1}{4a}\right) \).
Para verificá-lo, consideremos um ponto \( P(X_0, aX_0^2) \) sobre a parábola. A distância do foco candidato \( F\left(0, \displaystyle \frac{1}{4a}\right) \) é:
\[ d(P,F) = \sqrt{X_0^2 + \left(aX_0^2 - \frac{1}{4a}\right)^2} \]
A distância da diretriz candidata \( Y = -\displaystyle \frac{1}{4a} \) é:
\[ d(P,d) = \left|aX_0^2 + \frac{1}{4a}\right| \]
Para \( a > 0 \), elevando ao quadrado e simplificando, verifica-se que \( d(P,F) = d(P,d) \) para cada ponto \( P \) da parábola.
Voltando ao sistema original, obtemos as coordenadas indicadas.
Parâmetro focal: A distância do vértice ao foco é \( p = \displaystyle \frac{1}{4|a|} \).
A Diretriz da Parábola
Definição. A diretriz é a reta fixa tal que cada ponto da parábola é equidistante da diretriz e do foco.
Equação da diretriz:
\[ y = -\frac{\Delta}{4a} - \frac{1}{4a} \]
Demonstração. Da verificação da equidistância para a forma canónica, a diretriz tem equação \( Y = -\displaystyle \frac{1}{4a} \) no sistema transladado. Voltando ao sistema original: \( y = Y - \displaystyle \frac{\Delta}{4a} = -\displaystyle \frac{1}{4a} - \displaystyle \frac{\Delta}{4a} \).
Propriedades da diretriz:
- É perpendicular ao eixo de simetria
- Encontra-se a distância \( p = \displaystyle \frac{1}{4|a|} \) do vértice, oposta ao foco
- A distância foco-diretriz é \( 2p = \displaystyle \frac{1}{2|a|} \)
O Eixo de Simetria
O eixo de simetria é a reta que passa pelo vértice e pelo foco, em relação à qual a parábola é perfeitamente simétrica. Para uma parábola com eixo vertical de equação \( y = ax^2 + bx + c \), o eixo de simetria tem equação \( x = -\displaystyle \frac{b}{2a} \).
Cada ponto da parábola tem um ponto simétrico em relação ao eixo de simetria. Se \( P(x_0, y_0) \) pertence à parábola, então também o ponto \( P'(2x_V - x_0, y_0) \) pertence à parábola, onde \( x_V \) é a abscissa do vértice.
Relações entre os Elementos
Sistema coordenado: Os três elementos formam um sistema com relações precisas:
- Vértice e foco encontram-se sobre o eixo de simetria \( x = -\displaystyle \frac{b}{2a} \)
- A diretriz é perpendicular ao eixo de simetria
- O vértice é equidistante do foco e da diretriz (distância = parâmetro focal \( p \))
- Se \( a > 0 \): foco acima do vértice, diretriz abaixo
- Se \( a < 0 \): foco abaixo do vértice, diretriz acima
Exemplo Completo
Consideremos a parábola de equação \( y = 2x^2 - 8x + 3 \). Determinemos todos os elementos característicos.
Em primeiro lugar, identificamos os coeficientes: \( a = 2 \), \( b = -8 \), \( c = 3 \). O discriminante é \( \Delta = b^2 - 4ac = 64 - 24 = 40 \).
O vértice tem coordenadas \( V\left(-\displaystyle \frac{(-8)}{2 \cdot 2}, -\displaystyle \frac{40}{4 \cdot 2}\right) = V(2, -5) \).
O eixo de simetria tem equação \( x = 2 \).
Uma vez que \( a = 2 \), o parâmetro focal é \( p = \displaystyle \frac{1}{4|a|} = \displaystyle \frac{1}{4 \cdot 2} = \displaystyle \frac{1}{8} \). Uma vez que \( a > 0 \), a parábola tem concavidade para cima, portanto o foco encontra-se acima do vértice: \( F\left(2, -5 + \displaystyle \frac{1}{8}\right) = F\left(2, -\displaystyle \frac{39}{8}\right) \).
A diretriz encontra-se abaixo do vértice a distância \( p \): \( y = -5 - \displaystyle \frac{1}{8} = -\displaystyle \frac{41}{8} \).
Formas Particulares
Forma canónica \( y = ax^2 \):
- Vértice: \( V(0, 0) \)
- Foco: \( F\left(0, \displaystyle \frac{1}{4a}\right) \)
- Diretriz: \( y = -\displaystyle \frac{1}{4a} \)
Forma transladada \( y = a(x - h)^2 + k \):
- Vértice: \( V(h, k) \)
- Foco: \( F\left(h, k + \displaystyle \frac{1}{4a}\right) \)
- Diretriz: \( y = k - \displaystyle \frac{1}{4a} \)
Equação da Parábola Conhecidos o Vértice e um Ponto
Quando são conhecidos o vértice da parábola e outro ponto que pertence à curva, é possível determinar univocamente a equação da parábola. Este método é particularmente útil nas aplicações práticas onde se conhecem o ponto de mínimo ou máximo de uma função quadrática e um valor específico assumido pela função.
Forma Geral com Vértice Atribuído
Dada uma parábola com vértice \( V(h, k) \), a equação mais conveniente a utilizar é a forma do vértice, que para uma parábola com eixo vertical se escreve como \( y = a(x - h)^2 + k \), onde \( a \) é o parâmetro a determinar que controla a abertura e orientação da parábola.
Procedimento para Parábolas com Eixo Vertical
Seja \( V(h, k) \) o vértice da parábola e seja \( P(x_0, y_0) \) um ponto pertencente à parábola com \( x_0 \neq h \). Substituindo as coordenadas do ponto \( P \) na equação \( y = a(x - h)^2 + k \), obtemos:
\[ y_0 = a(x_0 - h)^2 + k \]
Desta equação podemos obter diretamente o valor do parâmetro \( a \):
\[ a = \frac{y_0 - k}{(x_0 - h)^2} \]
Uma vez determinado \( a \), a equação completa da parábola torna-se \( y = \displaystyle \frac{y_0 - k}{(x_0 - h)^2}(x - h)^2 + k \).
Exemplo Numérico - Eixo Vertical
Determinemos a equação da parábola com vértice \( V(3, -2) \) e que passa pelo ponto \( P(5, 6) \).
Utilizamos a forma do vértice \( y = a(x - 3)^2 - 2 \) e substituímos as coordenadas do ponto \( P(5, 6) \):
\[ 6 = a(5 - 3)^2 - 2 \]
\[ 6 = a \cdot 4 - 2 \]
\[ 8 = 4a \]
\[ a = 2 \]
A equação da parábola é portanto \( y = 2(x - 3)^2 - 2 \). Desenvolvendo esta expressão obtemos \( y = 2(x^2 - 6x + 9) - 2 = 2x^2 - 12x + 18 - 2 = 2x^2 - 12x + 16 \).
Para verificar a correção, controlamos que o vértice seja efetivamente \( V(3, -2) \). A abscissa do vértice é \( x_V = -\displaystyle \frac{b}{2a} = -\displaystyle \frac{-12}{2 \cdot 2} = 3 \) e a ordenada é \( y_V = 2 \cdot 3^2 - 12 \cdot 3 + 16 = 18 - 36 + 16 = -2 \).
Procedimento para Parábolas com Eixo Horizontal
Para parábolas com eixo horizontal, a equação na forma do vértice torna-se \( x = a(y - k)^2 + h \), onde \( V(h, k) \) é o vértice. Dado um ponto \( P(x_0, y_0) \) pertencente à parábola com \( y_0 \neq k \), o parâmetro \( a \) determina-se com:
\[ a = \frac{x_0 - h}{(y_0 - k)^2} \]
Relação com o Parâmetro Focal
Uma vez determinado o coeficiente \( a \), é possível calcular todos os outros elementos característicos da parábola. O parâmetro focal é \( p = \displaystyle \frac{1}{4|a|} \), a distância do vértice ao foco. O foco encontra-se no ponto \( F(h, k + p) \) para parábolas com eixo vertical e \( a > 0 \), enquanto se encontra em \( F(h, k - p) \) se \( a < 0 \).
Exercícios Resolvidos sobre a Parábola
Exercício 1. Dada a parábola de equação \( y = 3x^2 - 12x + 7 \), determinar vértice, foco, diretriz e parâmetro focal.
Solução. Da forma geral \( y = ax^2 + bx + c \) identificamos os coeficientes \( a = 3 \), \( b = -12 \), \( c = 7 \).
O vértice é dado pela fórmula \[ V\left(-\frac{b}{2a}, -\frac{\Delta}{4a}\right) \] onde \( \Delta = b^2 - 4ac = (-12)^2 - 4(3)(7) = 144 - 84 = 60 \). Substituindo:
\[ V\left(-\frac{-12}{2 \cdot 3}, -\frac{60}{4 \cdot 3}\right) = V\left(2, -5\right) \]
O parâmetro focal é \[ p = \frac{1}{4|a|} = \frac{1}{4 \cdot 3} = \frac{1}{12} \]
Uma vez que \( a = 3 > 0 \), a parábola tem concavidade para cima e o foco encontra-se acima do vértice:
\[ F\left(2, -5 + \frac{1}{12}\right) = F\left(2, -\frac{59}{12}\right) \]
A diretriz está posicionada abaixo do vértice à mesma distância do foco:
\[ y = -5 - \frac{1}{12} = -\frac{61}{12} \]
Exercício 2. Determinar a equação da parábola com eixo vertical que tem vértice \( V(-1, 4) \) e passa pelo ponto \( P(2, -5) \).
Solução. Utilizamos a forma do vértice \( y = a(x - h)^2 + k \) onde \( V(h, k) = (-1, 4) \):
\[ y = a(x - (-1))^2 + 4 = a(x + 1)^2 + 4 \]
Para determinar o parâmetro \( a \), substituímos as coordenadas do ponto \( P(2, -5) \):
\[ -5 = a(2 + 1)^2 + 4 \]
\[ -5 = 9a + 4 \]
\[ a = \frac{-9}{9} = -1 \]
A equação da parábola é portanto \( y = -(x + 1)^2 + 4 \).
Desenvolvendo a expressão obtemos a forma padrão:
\[ y = -(x^2 + 2x + 1) + 4 = -x^2 - 2x + 3 \]
Exercício 3. Dada a parábola com eixo horizontal \( x = 2y^2 - 8y + 6 \), determinar vértice, foco e diretriz.
Solução. Para identificar o vértice, completamos o quadrado em relação à variável \( y \):
\begin{align} x &= 2(y^2 - 4y) + 6 \\ &= 2(y^2 - 4y + 4 - 4) + 6 \\ &= 2(y - 2)^2 - 8 + 6 \\ &= 2(y - 2)^2 - 2 \end{align}
Da forma \( x = a(y - k)^2 + h \) lemos diretamente o vértice \( V(h, k) = V(-2, 2) \).
O parâmetro focal é \[ p = \frac{1}{4|a|} = \frac{1}{4 \cdot 2} = \frac{1}{8} \]
Uma vez que \( a = 2 > 0 \), a parábola abre-se para a direita e o foco encontra-se à direita do vértice:
\[ F\left(-2 + \frac{1}{8}, 2\right) = F\left(-\frac{15}{8}, 2\right) \]
A diretriz é a reta vertical posicionada à esquerda do vértice:
\[ x = -2 - \frac{1}{8} = -\frac{17}{8} \]
Exercício 4. Dada a parábola \( y = -2x^2 + 8x - 5 \), determinar a equação da parábola simétrica em relação ao eixo das abscissas. Calcular também os pontos de interseção entre as duas parábolas.
Solução. A parábola simétrica em relação ao eixo das abscissas obtém-se mudando o sinal da variável \( y \). Da equação original \( y = -2x^2 + 8x - 5 \), a parábola simétrica tem equação:
\[ y = 2x^2 - 8x + 5 \]
Para encontrar os pontos de interseção, resolvemos o sistema formado pelas duas parábolas:
\[ \begin{cases} y = -2x^2 + 8x - 5 \\ y = 2x^2 - 8x + 5 \end{cases} \]
Igualando as duas expressões:
\[ -2x^2 + 8x - 5 = 2x^2 - 8x + 5 \]
\[ -4x^2 + 16x - 10 = 0 \]
\[ -2(2x^2 - 8x + 5) = 0 \]
\[ 2x^2 - 8x + 5 = 0 \]
Aplicando a fórmula quadrática:
\[ x = \frac{8 \pm \sqrt{64 - 40}}{4} = \frac{8 \pm \sqrt{24}}{4} = \frac{8 \pm 2\sqrt{6}}{4} = \frac{4 \pm \sqrt{6}}{2} \]
As ordenadas correspondentes calculam-se substituindo numa das duas equações:
Para \( x_1 = \displaystyle \frac{4 + \sqrt{6}}{2} \) : \( y_1 = 2\left(\displaystyle \frac{4 + \sqrt{6}}{2}\right)^2 - 8\left(\displaystyle \frac{4 + \sqrt{6}}{2}\right) + 5 = -\displaystyle \frac{1}{2} \)
Para \( x_2 = \displaystyle \frac{4 - \sqrt{6}}{2} \) : \( y_2 = 2\left(\displaystyle \frac{4 - \sqrt{6}}{2}\right)^2 - 8\left(\displaystyle \frac{4 - \sqrt{6}}{2}\right) + 5 = -\displaystyle \frac{1}{2} \)
Os pontos de interseção são:
\[ A\left(\frac{4 + \sqrt{6}}{2}, -\frac{1}{2}\right) \quad \text{e} \quad B\left(\frac{4 - \sqrt{6}}{2}, -\frac{1}{2}\right) \]
Estando ambos os pontos à mesma ordenada, a distância entre eles é simplesmente:
\[ d(A,B) = \left|\frac{4 + \sqrt{6}}{2} - \frac{4 - \sqrt{6}}{2}\right| = \left|\frac{2\sqrt{6}}{2}\right| = \sqrt{6} \]
Exercício 5. Determinar a equação da parábola com eixo vertical que tem foco \( F(1, 5) \) e diretriz \( y = 3 \). Verificar se o ponto \( P(3, 6) \) pertence à parábola.
Solução. O vértice da parábola é o ponto equidistante do foco e da diretriz, situado sobre a reta perpendicular à diretriz e que passa pelo foco. Uma vez que a diretriz é horizontal, o vértice tem a mesma abscissa do foco e ordenada igual à média aritmética:
\[ V\left(1, \frac{5 + 3}{2}\right) = V(1, 4) \]
O parâmetro focal é a distância do vértice ao foco:
\[ p = |5 - 4| = 1 \]
O coeficiente da parábola é portanto:
\[ a = \frac{1}{4p} = \frac{1}{4 \cdot 1} = \frac{1}{4} \]
A equação da parábola na forma do vértice é:
\[ y = \frac{1}{4}(x - 1)^2 + 4 \]
Para verificar se \( P(3, 6) \) pertence à parábola, substituímos as suas coordenadas:
\[ y = \frac{1}{4}(3 - 1)^2 + 4 = \frac{1}{4} \cdot 4 + 4 = 1 + 4 = 5 \neq 6 \]
Confirmamos o resultado utilizando a definição geométrica da parábola. A distância de P ao foco é:
\[ d(P,F) = \sqrt{(3-1)^2 + (6-5)^2} = \sqrt{4 + 1} = \sqrt{5} \]
A distância de P à diretriz é:
\[ d(P, \text{diretriz}) = |6 - 3| = 3 \]
Uma vez que \( \sqrt{5} \neq 3 \), o ponto \( P(3, 6) \) não pertence à parábola.

