O estudo das posições relativas entre duas retas é um dos temas fundamentais da geometria analítica plana. Compreender como duas retas podem se posicionar no plano cartesiano permite classificar com precisão todas as situações geométricas possíveis: desde a intersecção num único ponto até a sobreposição completa.
Índice
- Representação das retas no plano
- Classificação das posições relativas
- Retas perpendiculares
- Exercícios resolvidos
Representação das retas no plano
Dadas duas retas no plano, podem apresentar-se três configurações principais:
- Retas coincidentes: trata-se de duas equações que descrevem na realidade a mesma reta. Neste caso, as retas têm todos os pontos em comum e são indistinguíveis do ponto de vista geométrico.
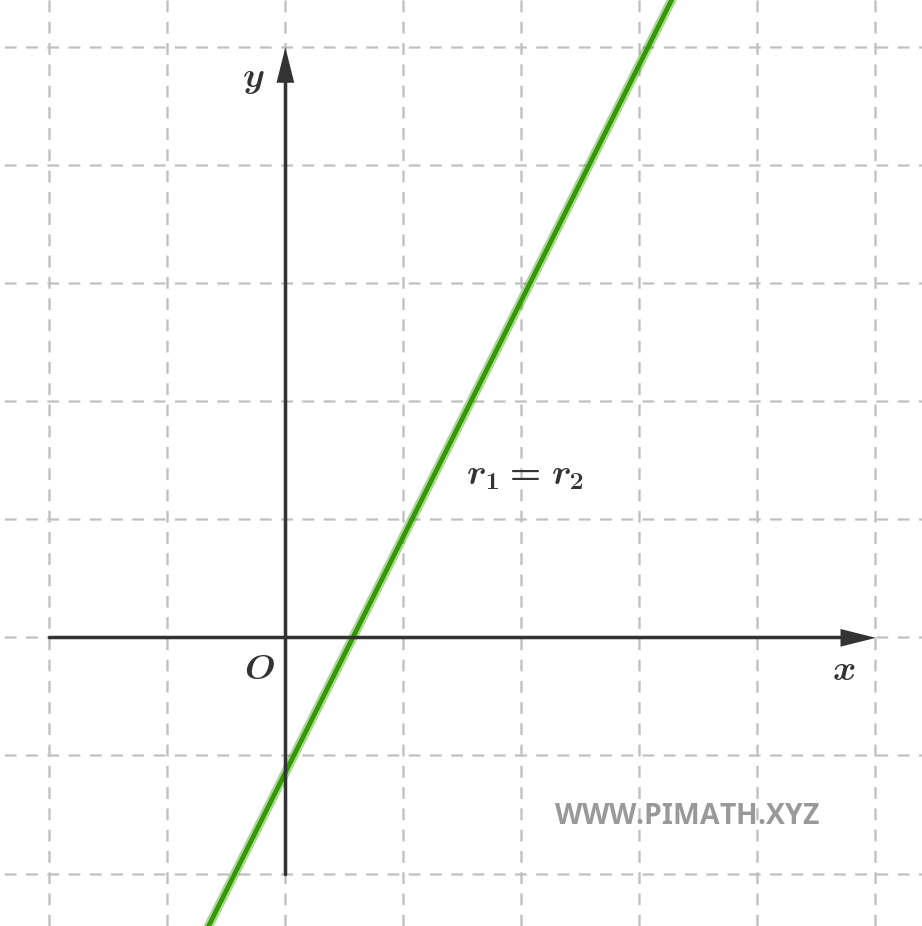
- Retas concorrentes: intersectam-se num só ponto do plano, formando um ângulo que pode assumir qualquer amplitude compreendida entre 0° e 180°, excluindo os casos de paralelismo.
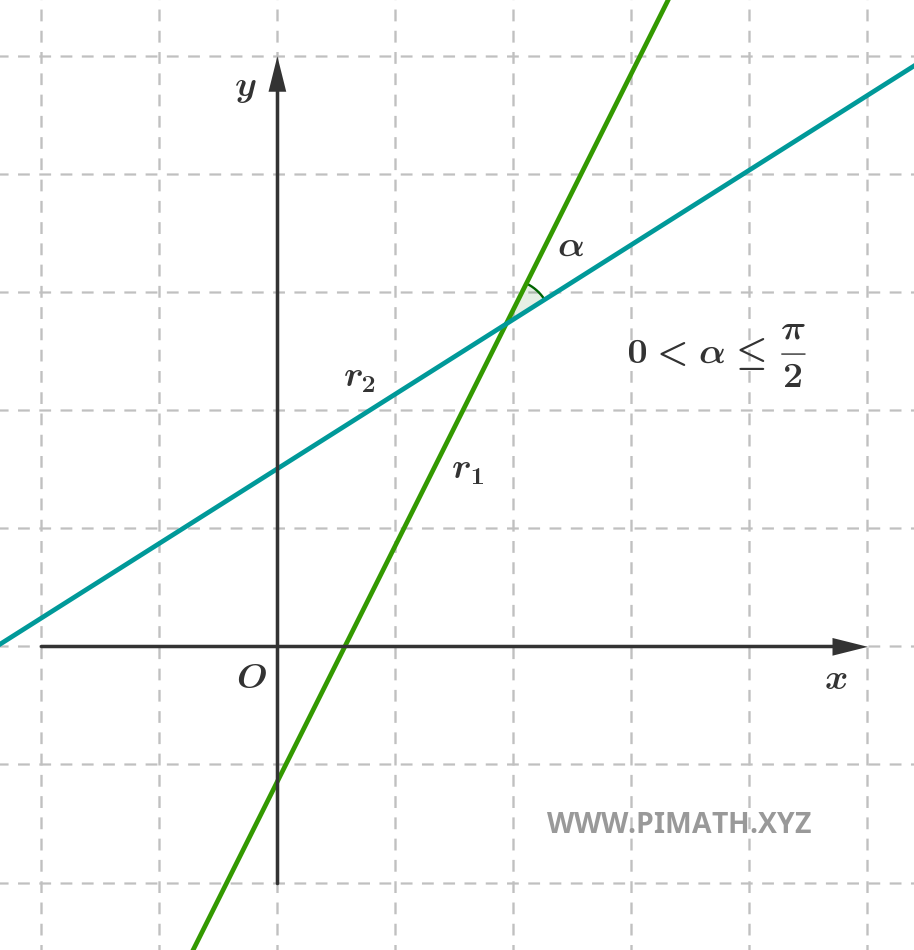
- Retas paralelas distintas: embora tenham a mesma inclinação (ou seja, o mesmo coeficiente angular), estas retas nunca se encontram. Não partilham nenhum ponto.
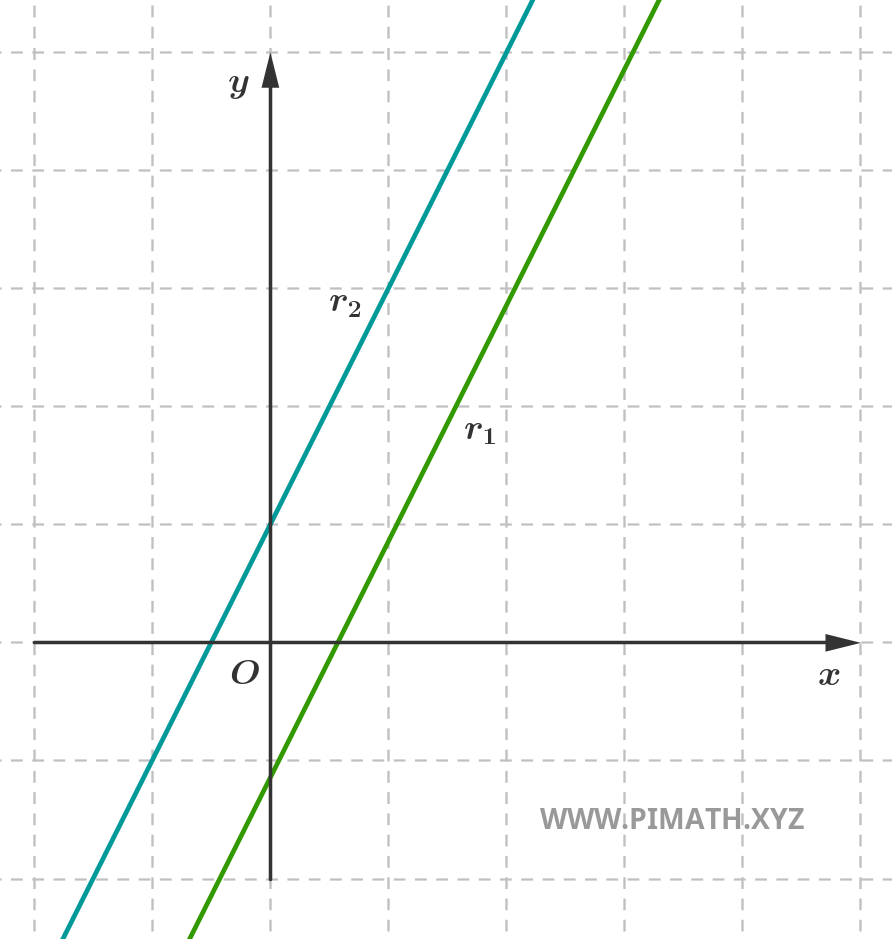
Dentro das retas concorrentes encontra-se um caso particular muito importante: o das retas perpendiculares. Duas retas são perpendiculares se se intersectam formando um ângulo reto \( \displaystyle \frac{\pi}{2} \) (ou seja, de 90°).
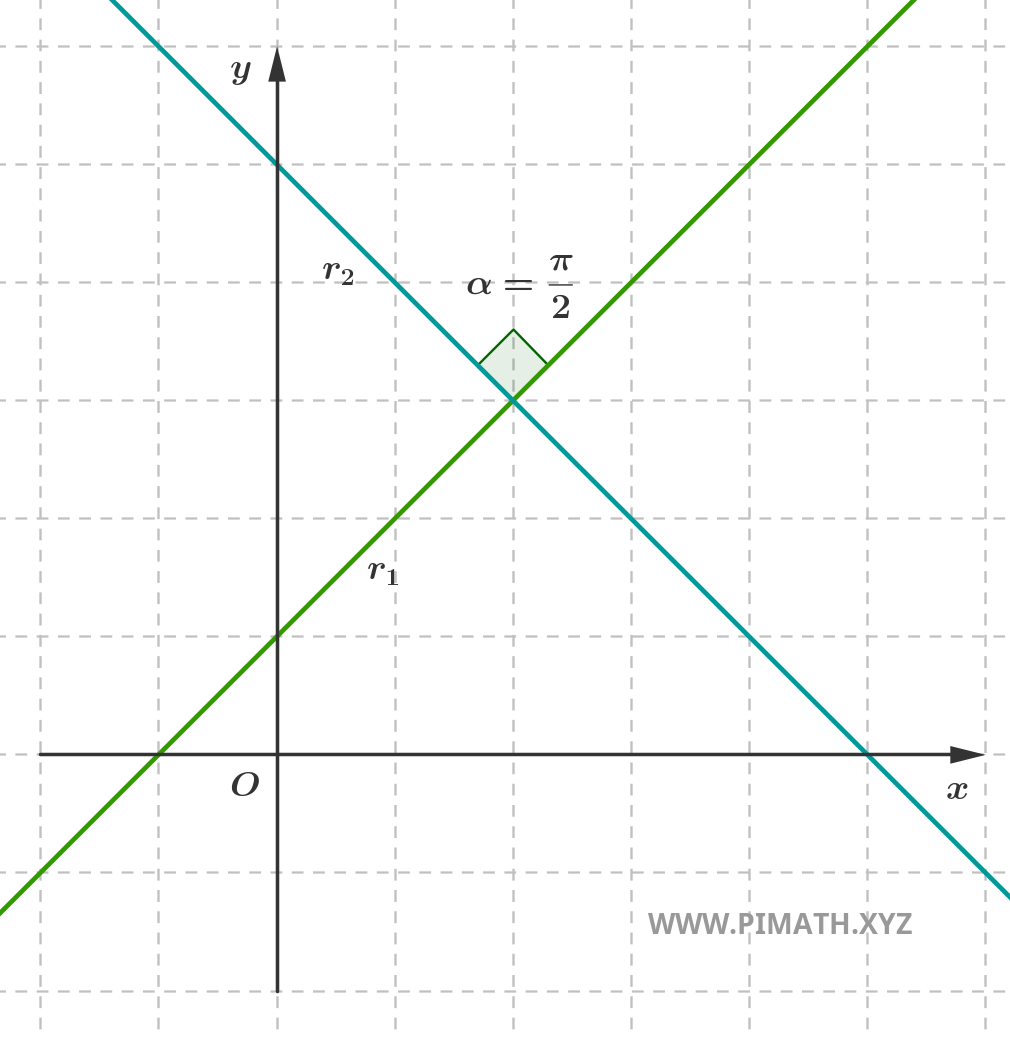
Formas da equação de uma reta
Uma reta no plano cartesiano pode ser representada de várias maneiras, equivalentes entre si mas úteis em contextos diferentes.
A forma explícita, também chamada forma reduzida, é talvez a mais intuitiva:
\[ y = mx + b \]
Nesta equação:
O parâmetro \( m \in \mathbb{R} \) denomina-se coeficiente angular ou declive e representa a inclinação da reta. Por convenção, se a reta é vertical, diz-se que o coeficiente angular é infinito ou não está definido.
O termo \( b \in \mathbb{R} \) é a ordenada na origem, ou seja, o ponto onde a reta intersecta o eixo \( y \).
Outra forma de escrita é a forma implícita, também chamada forma geral:
\[ ax + by + c = 0 \]
Neste caso, \( a, b, c \in \mathbb{R} \), e deve ter-se \( a^2 + b^2 \neq 0 \) para que se trate efetivamente da equação de uma reta.
Relação entre as formas
Quando o coeficiente \( b \) é diferente de zero, é possível obter a forma explícita a partir da implícita. Com efeito, resolvendo em ordem a \( y \), obtém-se:
\[ ax + by + c = 0 \quad \Leftrightarrow \quad y = -\frac{a}{b}x - \frac{c}{b} \]
Desta forma, o coeficiente angular resulta \( m = -\displaystyle \frac{a}{b} \) e a ordenada na origem é \( b = -\displaystyle \frac{c}{b} \).
Se em vez disso \( b = 0 \) e \( a \neq 0 \), a equação reduz-se à forma \( x = -\displaystyle \frac{c}{a} \), que representa uma reta vertical. Neste caso, o coeficiente angular não está definido.
Classificação das posições relativas
Retas coincidentes
Duas retas são coincidentes quando coincidem ponto por ponto: cada ponto de uma pertence também à outra. Em substância, trata-se da mesma reta expressa com duas equações proporcionais.
Se estão expressas em forma explícita, tem-se:
\[ r: y = mx + b \quad \text{e} \quad s: y = mx + b \]
Em forma implícita, duas retas \( r: a_1x + b_1y + c_1 = 0 \) e \( s: a_2x + b_2y + c_2 = 0 \) são coincidentes se e só se existe uma constante \( k \neq 0 \) tal que:
\[ \frac{a_1}{a_2} = \frac{b_1}{b_2} = \frac{c_1}{c_2} = k \]
Equivalentemente, isto significa que \( (a_2, b_2, c_2) = k(a_1, b_1, c_1) \) para algum \( k \neq 0 \).
Exemplo: as retas \( 2x + 3y - 6 = 0 \) e \( 4x + 6y - 12 = 0 \) são coincidentes, porque os coeficientes de uma são o dobro dos da outra:
\[ \frac{2}{4} = \frac{3}{6} = \frac{-6}{-12} = \frac{1}{2} \]
Retas paralelas
Duas retas são paralelas se têm a mesma direção. No caso de não coincidirem, dizem-se paralelas distintas e não têm pontos em comum.
Em forma explícita, a condição de paralelismo é:
\[ m_1 = m_2 \]
Se além disso \( b_1 \neq b_2 \), então as retas são paralelas distintas.
Em forma implícita, duas retas \( r: a_1x + b_1y + c_1 = 0 \) e \( s: a_2x + b_2y + c_2 = 0 \) são paralelas se e só se:
\[ a_1b_2 - a_2b_1 = 0 \]
Isto equivale a dizer que \( \displaystyle \frac{a_1}{a_2} = \displaystyle \frac{b_1}{b_2} \) (quando \( a_2, b_2 \neq 0 \)).
Para ter paralelismo distinto, deve verificar-se ainda que:
\[ \frac{c_1}{c_2} \neq \frac{a_1}{a_2} \quad \text{(ou seja} \quad \frac{c_1}{c_2} \neq \frac{b_1}{b_2}\text{)} \]
Exemplo: as retas \( r: y = 3x + 2 \) e \( s: y = 3x - 1 \) são paralelas distintas porque têm o mesmo coeficiente angular mas diferente ordenada na origem.
Retas concorrentes
Duas retas são concorrentes se se intersectam num único ponto. Isto acontece quando as retas têm direções diferentes, ou seja, coeficientes angulares distintos (no caso de retas não verticais).
Em forma explícita, basta verificar que:
\[ m_1 \neq m_2 \]
Em forma implícita, a condição é:
\[ a_1b_2 - a_2b_1 \neq 0 \]
Ponto de intersecção
Para determinar o ponto de intersecção entre duas retas concorrentes expressas em forma implícita, resolve-se o seguinte sistema linear:
\[ \begin{cases} a_1x + b_1y + c_1 = 0 \\ a_2x + b_2y + c_2 = 0 \end{cases} \]
Aplicando a regra de Cramer, as coordenadas do ponto de intersecção são:
\[ x = \frac{b_1c_2 - b_2c_1}{a_1b_2 - a_2b_1}, \quad y = \frac{a_2c_1 - a_1c_2}{a_1b_2 - a_2b_1} \]
desde que \( a_1b_2 - a_2b_1 \neq 0 \).
Retas perpendiculares
Condição de perpendicularidade
Duas retas são perpendiculares se se intersectam formando um ângulo reto, ou seja, de 90°.
Em forma explícita, se as retas têm coeficientes angulares \( m_1 \) e \( m_2 \) finitos, a condição é:
\[ m_1 \cdot m_2 = -1 \]
Caso particular: uma reta horizontal (\( m = 0 \)) é perpendicular a uma reta vertical (coeficiente angular não definido).
Em forma implícita, duas retas \( r: a_1x + b_1y + c_1 = 0 \) e \( s: a_2x + b_2y + c_2 = 0 \) são perpendiculares se e só se:
\[ a_1a_2 + b_1b_2 = 0 \]
Esta relação deriva do facto de os vetores normais das duas retas, \( \vec{n}_1 = (a_1, b_1) \) e \( \vec{n}_2 = (a_2, b_2) \), resultarem ortogonais, ou seja, o seu produto escalar é nulo.
Demonstração analítica
O ângulo \( \theta \) entre duas retas de coeficientes angulares \( m_1 \) e \( m_2 \) é expresso pela fórmula:
\[ \tan(\theta) = \left| \frac{m_2 - m_1}{1 + m_1m_2} \right| \]
onde \( \theta \) representa o ângulo agudo entre as duas retas.
Se \( m_1m_2 = -1 \), o denominador \( 1 + m_1m_2 \) anula-se e a tangente torna-se indefinida, o que corresponde a um ângulo de 90°.
Exercícios resolvidos
Exercício 1. Estabelecer se as retas \( r: y = -2x + 1 \) e \( s: y = \displaystyle \frac{1}{2}x - 3 \) são perpendiculares.
Determinemos os coeficientes angulares:
\[ m_1 = -2 \]
\[ m_2 = \frac{1}{2} \]
Verifiquemos o produto entre os dois coeficientes:
\[ m_1 \cdot m_2 = (-2) \cdot \frac{1}{2} = -1 \]
Visto que o produto é igual a -1, podemos concluir que as duas retas são perpendiculares.
Exercício 2. Calcular o ângulo agudo entre as retas \( r: y = 2x \) e \( s: y = -x \).
Os coeficientes angulares são:
\[ m_1 = 2 \]
\[ m_2 = -1 \]
Utilizemos a fórmula para o cálculo do ângulo agudo \( \theta \) entre duas retas:
\[ \tan(\theta) = \left| \frac{m_2 - m_1}{1 + m_1 m_2} \right| = \left| \frac{-1 - 2}{1 + 2 \cdot (-1)} \right| = \left| \frac{-3}{1 - 2} \right| = \left| \frac{-3}{-1} \right| = 3 \]
Portanto:
\[ \theta = \arctan(3) \approx 71{,}57^\circ \]
Exercício 3. Encontrar a equação da reta perpendicular a \( r: y = -\displaystyle \frac{3}{2}x + 4 \) e que passa pelo ponto \( P(2, 1) \).
O coeficiente angular da reta dada é \( m = -\displaystyle \frac{3}{2} \).
O coeficiente angular da reta perpendicular será o oposto do recíproco:
\[ m' = -\frac{1}{m} = -\frac{1}{-\frac{3}{2}} = \frac{2}{3} \]
Utilizemos a fórmula do feixe próprio de retas que passam por \( P(2, 1) \):
\[ y - y_0 = m'(x - x_0) \quad \text{com } (x_0, y_0) = (2, 1) \] \[ y - 1 = \frac{2}{3}(x - 2) \] \[ y = \frac{2}{3}x - \frac{4}{3} + 1 = \frac{2}{3}x - \frac{1}{3} \]
A equação procurada é:
\[ y = \frac{2}{3}x - \frac{1}{3} \]
Exercício 4. Determinar o valor de \( k \) para que as retas \( r: 2x + 3y - 1 = 0 \) e \( s: kx + 6y + 2 = 0 \) sejam paralelas.
Duas retas em forma implícita são paralelas se \( a_1b_2 - a_2b_1 = 0 \).
Identifiquemos os coeficientes:
- Reta \( r \): \( a_1 = 2, b_1 = 3, c_1 = -1 \)
- Reta \( s \): \( a_2 = k, b_2 = 6, c_2 = 2 \)
Apliquemos a condição:
\[ a_1b_2 - a_2b_1 = 2 \cdot 6 - k \cdot 3 = 12 - 3k = 0 \] \[ 3k = 12 \quad \Rightarrow \quad k = 4 \]
Verifiquemos que para \( k = 4 \) as retas são efetivamente paralelas distintas:
\[ \frac{a_1}{a_2} = \frac{2}{4} = \frac{1}{2} \]
\[ \frac{b_1}{b_2} = \frac{3}{6} = \frac{1}{2} \]
\[ \frac{c_1}{c_2} = \frac{-1}{2} = -\frac{1}{2} \]
Visto que \( \displaystyle \frac{a_1}{a_2} = \displaystyle \frac{b_1}{b_2} \neq \displaystyle \frac{c_1}{c_2} \), as retas são paralelas distintas para \( k = 4 \).
Exercício 5. Determinar o ponto de intersecção entre as retas:
\( r: x + 2y - 3 = 0 \)
\( s: 2x - y + 1 = 0 \)
Resolvamos o sistema:
\[ \begin{cases} x + 2y = 3 \\ 2x - y = -1 \end{cases} \]
Utilizemos o método de eliminação. Multipliquemos a segunda equação por 2:
\[ \begin{cases} x + 2y = 3 \\ 4x - 2y = -2 \end{cases} \]
Somemos as duas equações:
\[ x + 4x + 2y - 2y = 3 + (-2) \] \[ 5x = 1 \quad \Rightarrow \quad x = \frac{1}{5} \]
Substituamos na primeira equação:
\[ \frac{1}{5} + 2y = 3 \quad \Rightarrow \quad 2y = 3 - \frac{1}{5} = \frac{15 - 1}{5} = \frac{14}{5} \] \[ y = \frac{7}{5} \]
O ponto de intersecção é:
\[ \left( \frac{1}{5}, \frac{7}{5} \right) \]
Verificação: substituindo em ambas as equações originais obtém-se a identidade \( 0 = 0 \), confirmando a correção do resultado.

