O Teorema de Rolle é um resultado fundamental aplicável a funções contínuas e diferenciáveis. Este teorema estabelece que, se uma função \( f \) é contínua em um intervalo fechado \([a,b]\), diferenciável no intervalo aberto \((a,b)\) e assume o mesmo valor nas extremidades \( f(a) = f(b) \), então existe pelo menos um ponto interno \( \xi \in (a,b) \) no qual a derivada da função se anula, ou seja, \( f'(\xi) = 0 \). Este resultado possui inúmeras aplicações, inclusive na demonstração do Teorema do Valor Médio.
Índice
Teorema de Rolle
Seja \( f : [a,b] \to \mathbb{R} \) uma função contínua no intervalo fechado \([a,b]\), diferenciável no intervalo aberto \((a,b)\) e tal que \( f(a) = f(b) \). Então existe pelo menos um ponto \( \xi \in (a,b) \) tal que: \[ f'(\xi) = 0 \]
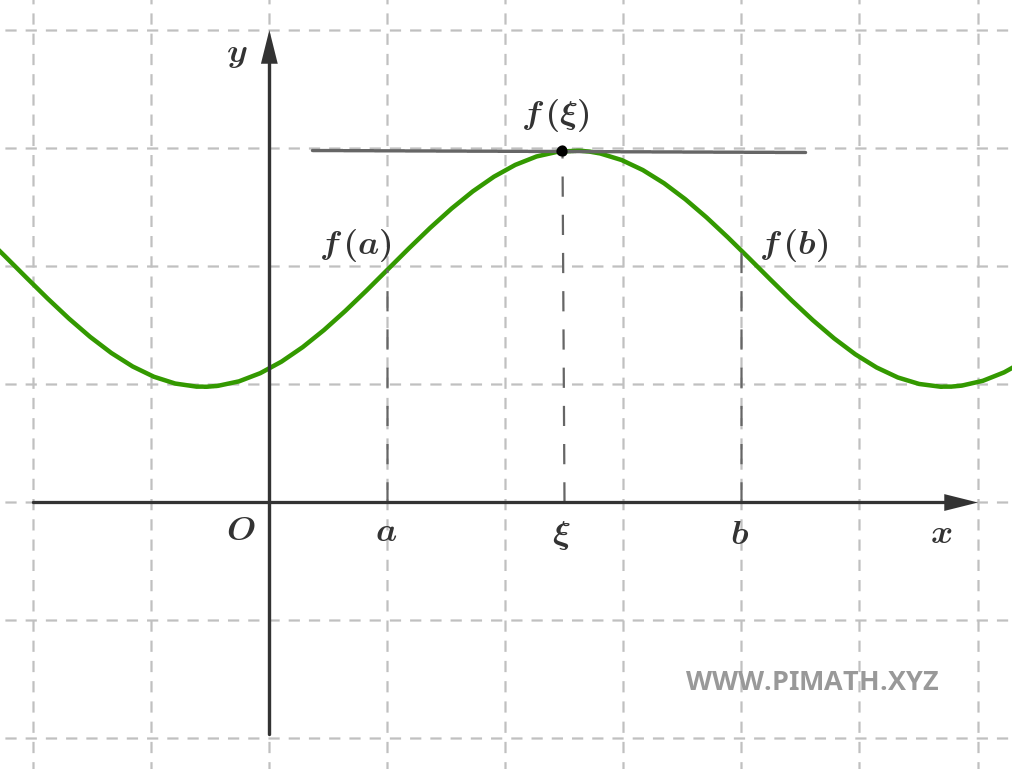
Demonstração. Em primeiro lugar, como \( f \) é contínua em \([a,b]\), pelo Teorema de Weierstrass ela admite máximo e mínimo absolutos no intervalo. Portanto, existem pontos \( c, d \in [a,b] \) tais que: \[ f(c) = M \quad \text{e} \quad f(d) = m \] onde \( M = \max_{x \in [a,b]} f(x) \) e \( m = \min_{x \in [a,b]} f(x) \).
Consideremos primeiramente o caso em que a função \( f \) seja constante, ou seja, \( f(x) = k \) para todo \( x \in [a,b] \). Nesse caso, pela definição de derivada: \[ f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} = \lim_{h \to 0} \frac{k - k}{h} = 0 \] para todo \( x \in (a,b) \). A afirmação está, portanto, imediatamente verificada.
Passamos agora ao caso em que \( f \) não seja constante. Como \( f(a) = f(b) \), o máximo e o mínimo absolutos não podem ocorrer ambos nas extremidades \( a \) e \( b \). Deve existir pelo menos um ponto \( \xi \in (a,b) \) em que \( f(\xi) = M \) ou \( f(\xi) = m \). Em ambos os casos, \( \xi \) representa um ponto de máximo ou mínimo local.
Seja \( \xi \) um ponto de máximo local. Para \( h \) suficientemente pequeno:
\[ f(\xi + h) \leq f(\xi) \]
Podemos, então, considerar os quocientes incrementais:
\[ \frac{f(\xi + h) - f(\xi)}{h} \leq 0 \quad \text{se} \ h > 0 \]
\[ \frac{f(\xi + h) - f(\xi)}{h} \geq 0 \quad \text{se} \ h < 0 \]
Como \( f \) é diferenciável em \( \xi \), existe o limite do quociente incremental, ou seja: \[ f'(\xi) = \lim_{h \to 0} \frac{f(\xi + h) - f(\xi)}{h} \]
Pelo exposto acima, temos:
\[ \lim_{h \to 0^+} \frac{f(\xi + h) - f(\xi)}{h} \leq 0 \leq \lim_{h \to 0^-} \frac{f(\xi + h) - f(\xi)}{h} \]
Portanto, necessariamente: \[ f'(\xi) = 0 \]
Um raciocínio análogo aplica-se no caso em que \( \xi \) seja um ponto de mínimo local.
Assim, demonstramos que existe pelo menos um ponto \( \xi \in (a,b) \) tal que \( f'(\xi) = 0 \), completando a demonstração do Teorema de Rolle.