Uma inequação do segundo grau é uma expressão algébrica que estabelece uma relação de ordem entre dois termos contendo uma variável do segundo grau. Pode ser escrita na forma:
\[ a x^2 + bx + c \leq 0 \quad \text{ou} \quad a x^2 + bx + c \geq 0 \]
onde \( a \) e \( b \) são coeficientes reais com \( a \neq 0 \) e \( x \) é a variável incógnita. Fala-se de inequação em sentido estrito se
\[ a x^2 + bx + c < 0 \quad \text{ou} \quad a x^2 + bx + c > 0 \]
- O que são as Inequações do Segundo Grau
- Princípios de Equivalência para as Inequações
- Como resolver as Inequações do Segundo Grau
O que são as Inequações do Segundo Grau
Uma inequação do segundo grau estabelece uma relação de ordem entre duas expressões algébricas, e a solução é representada por um intervalo de valores que verificam a desigualdade. Em outras palavras, o conjunto das soluções de uma inequação do segundo grau não são dois valores, mas um intervalo ou a união de intervalos de números reais.
Princípios de Equivalência para as Inequações do Segundo Grau
A resolução de uma inequação do segundo grau baseia-se em dois princípios fundamentais:
Primeiro Princípio de Equivalência
O princípio de equivalência para as inequações do segundo grau afirma que se se somar ou subtrair o mesmo número a ambos os membros de uma inequação, a relação de ordem não muda. Por exemplo:
Se \( a x^2 + b x + c \leq 0 \), então podemos somar \( d \) a ambos os membros e obter:
\[ (a x^2 + b x + c) + d \leq 0 + d \]
Segundo Princípio de Equivalência
O segundo princípio de equivalência afirma que se se multiplicar ou dividir ambos os membros de uma inequação por um número positivo, a relação de ordem não muda. Entretanto, se se multiplicar ou dividir por um número negativo, a inequação deve ser invertida. Eis alguns exemplos:
Se \( a x^2 + b x + c \leq 0 \) e multiplicamos ambos os membros por um número positivo \( k \), obtemos:
\[ k(a x^2 + b x + c) \leq k \cdot 0 \]
Se, ao contrário, multiplicamos por um número negativo \( k \), a inequação torna-se:
\[ k(a x^2 + b x + c) \geq k \cdot 0 \]
Quando se multiplica ou se divide ambos os membros de uma inequação do segundo grau por um número negativo, é preciso inverter o sinal da inequação. Por exemplo:
Se \( -2 x^2 + 4 x \leq 6 \), dividindo ambos os membros por \( -2 \), devemos inverter o sinal da inequação:
\[ x^2 - 2 x \geq -3 \]
Como resolver as Inequações do Segundo Grau
O primeiro passo é reescrever a inequação em forma canónica, portanto levamos todos os termos ao primeiro membro:
\[ ax^2+bx+c \leq 0 \quad \text{ou} \quad ax^2+bx+c \geq 0 \]
\[ ax^2+bx+c < 0 \quad \text{ou} \quad ax^2+bx+c > 0 \]
conforme se trate de uma desigualdade ou desigualdade em sentido estrito.
Neste ponto, devemos calcular as raízes (ou soluções) da equação associada, utilizando a fórmula resolutiva para as equações do segundo grau:
\[ x_{1,2} = \frac{-b \pm \sqrt{\Delta}}{2a}, \quad \text{com} \quad \Delta = b^2 - 4ac \]
As soluções obtidas permitir-nos-ão determinar os intervalos nos quais a inequação é verificada, ou seja, os valores de \(x\) para os quais a inequação é satisfeita, tanto dentro como fora de tais intervalos.
O sinal do discriminante \( \Delta \) permite-nos compreender a natureza das soluções: se \( \Delta > 0 \), há duas soluções reais distintas; se \( \Delta = 0 \), há duas soluções reais coincidentes; se \( \Delta < 0 \), não há soluções reais.
Resolução da inequação:
Se o coeficiente quadrático da equação associada for maior que zero, então as soluções serão:
- \( (x_1, x_2) \) se a inequação que queremos estudar é
\[ ax^2+bx+c < 0 \quad , \quad a > 0 \]
- \( (-\infty, x_1) \cup (x_2, +\infty) \) se a inequação que queremos estudar é
\[ ax^2+bx+c > 0 \quad , \quad a > 0 \]
- \( [x_1, x_2] \) se a inequação que queremos estudar é
\[ ax^2+bx+c \leq 0 \quad , \quad a > 0 \]
- \( (-\infty, x_1] \cup [x_2, +\infty) \) se a inequação que queremos estudar é
\[ ax^2+bx+c \geq 0 \quad , \quad a > 0 \]
No caso em que o coeficiente quadrático seja negativo (\(a < 0\)), os intervalos de solução serão invertidos:
- \( (-\infty, x_1) \cup (x_2, +\infty) \) se a inequação que queremos estudar é
\[ ax^2+bx+c < 0 \quad , \quad a < 0 \]
- \( (x_1, x_2) \) se a inequação que queremos estudar é
\[ ax^2+bx+c > 0 \quad , \quad a < 0 \]
- \( (-\infty, x_1] \cup [x_2, +\infty) \) se a inequação que queremos estudar é
\[ ax^2+bx+c \leq 0 \quad , \quad a < 0 \]
- \( [x_1, x_2] \) se a inequação que queremos estudar é
\[ ax^2+bx+c \geq 0 \quad , \quad a < 0 \]
Como veremos na secção dedicada à representação gráfica, não precisará de aprender essas regras de memória.
Exemplos Práticos com Explicações Passo a Passo
Vejamos alguns exemplos de resolução de uma inequação do segundo grau.
Exercício 1. Encontrar os valores para os quais a seguinte inequação \( x^2 - 5x \leq -6 \) é verdadeira.
Solução. Para resolver essa inequação, seguimos os passos fundamentais. Primeiro, levamos tudo ao primeiro membro de modo a obter a forma canónica:
\[ x^2 - 5x + 6 \leq 0 \]
Agora calculamos o discriminante da equação associada. Considerando a expressão \( x^2 - 5x + 6 \), obtemos:
\[ \Delta = (-5)^2 - 4(1)(6) = 25 - 24 = 1 \]
O discriminante é positivo, portanto a equação tem duas soluções reais distintas. Resolvendo a equação associada \( x^2 - 5x + 6 = 0 \), encontramos os valores:
\[ x_{1,2} = \frac{-(-5) \pm \sqrt{1}}{2(1)} = \frac{5 \pm 1}{2} \]
portanto \( x_1 = 2 \) e \( x_2 = 3 \).
Visto que o coeficiente do termo \( x^2 \) é positivo, a parábola tem a concavidade voltada para cima e a inequação será satisfeita no intervalo compreendido entre as duas soluções.
As soluções \( 2 \leq x \leq 3 \) podem ser representadas graficamente da seguinte forma:
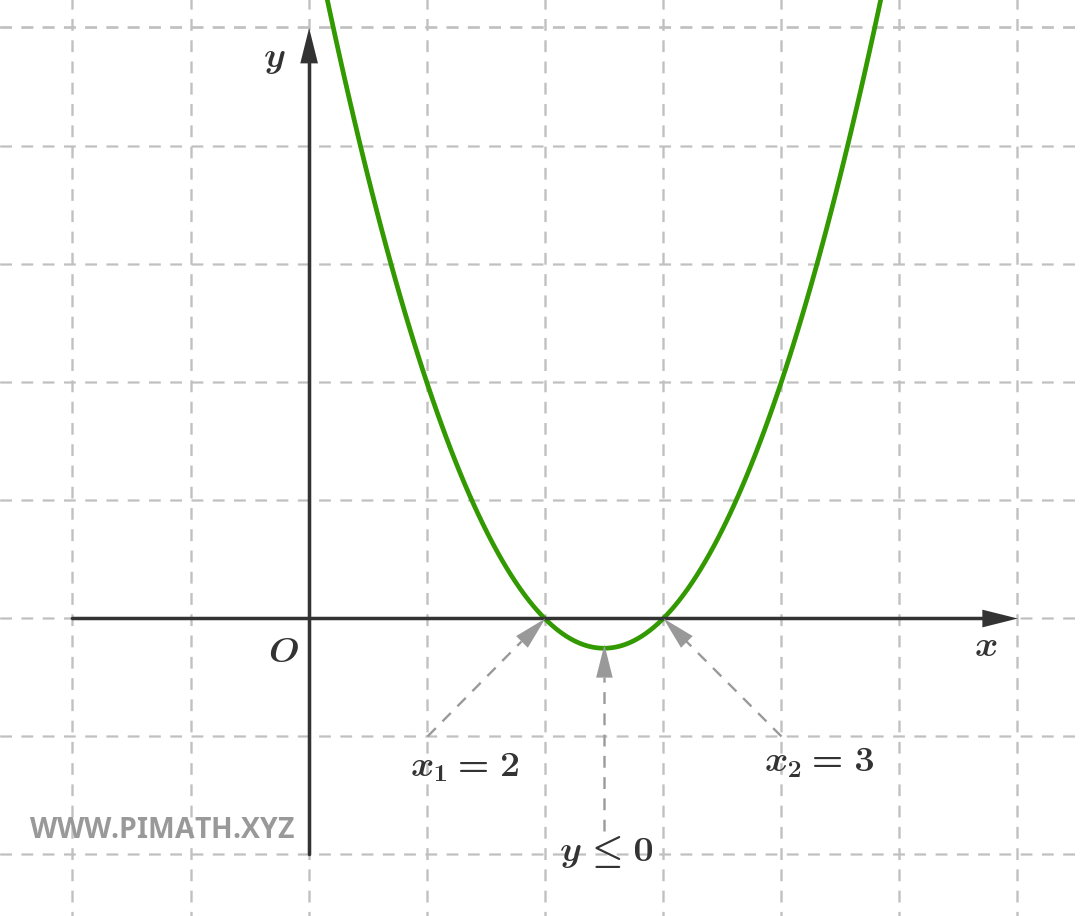
Habitualmente, para evitar desenhar sempre a parábola, prefere-se representar as soluções numa reta, distinguindo os valores positivos com uma linha contínua e os negativos com uma linha tracejada. Por exemplo, as soluções da inequação anterior são representadas desta forma:
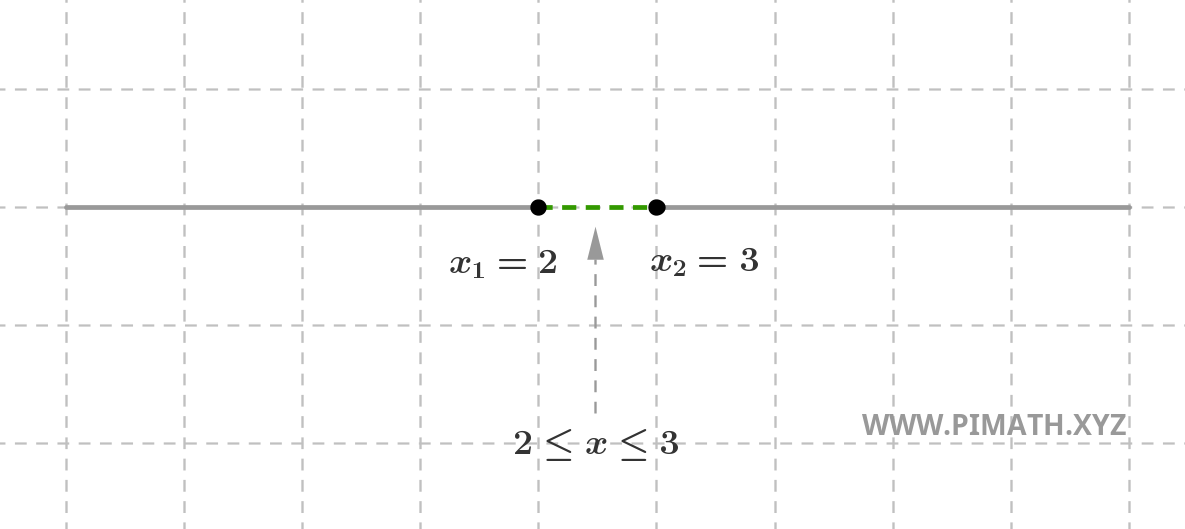
Atenção à inclusão das soluções: Se estivermos a estudar uma inequação em sentido estrito (\( < \) ou \( > \)), as raízes da equação associada devem ser excluídas, e isso representa-se com círculos vazios na representação gráfica. Se, pelo contrário, a inequação é em sentido amplo (\( \leq \) ou \( \geq \)), as raízes são incluídas e indicam-se com círculos cheios.
Exercício 2. Resolver a inequação do segundo grau \( 2x^2 - 4x - 6 > 0 \)
Solução. Calculamos o discriminante \( \Delta = b^2 - 4ac \)
Para essa equação, \( a = 2 \), \( b = -4 \), e \( c = -6 \). Substituindo esses valores na fórmula:
\[ \Delta = (-4)^2 - 4(2)(-6) = 16 + 48 = 64 \]
Visto que \( \Delta > 0 \), a equação tem duas soluções reais distintas.
A fórmula resolutiva para a equação associada é:
\[ x_{1,2} = \frac{-b \pm \sqrt{\Delta}}{2a} \]
Substituindo \( b = -4 \), \( \Delta = 64 \), e \( a = 2 \) na fórmula:
\[ x_{1,2} = \frac{4 \pm \sqrt{64}}{2 \times 2} = \frac{4 \pm 8}{4} \]
A primeira solução é \( x_1 = \displaystyle \frac{4 - 8}{4} = \displaystyle \frac{-4}{4} = -1 \), a segunda solução é, pelo contrário, \( x_2 = \displaystyle \frac{4 + 8}{4} = \displaystyle \frac{12}{4} = 3 \).
As soluções da equação são portanto:
\[ x_1 = -1 \quad \text{e} \quad x_2 = 3 \]
Note que o coeficiente quadrático é maior que zero e a inequação pede as soluções para as quais se tem \( ax^2+bx+c > 0 \), portanto as soluções positivas encontram-se "externas ao intervalo", isto é \( x < -1 \) ou \( x > 3 \), como mostra o gráfico:
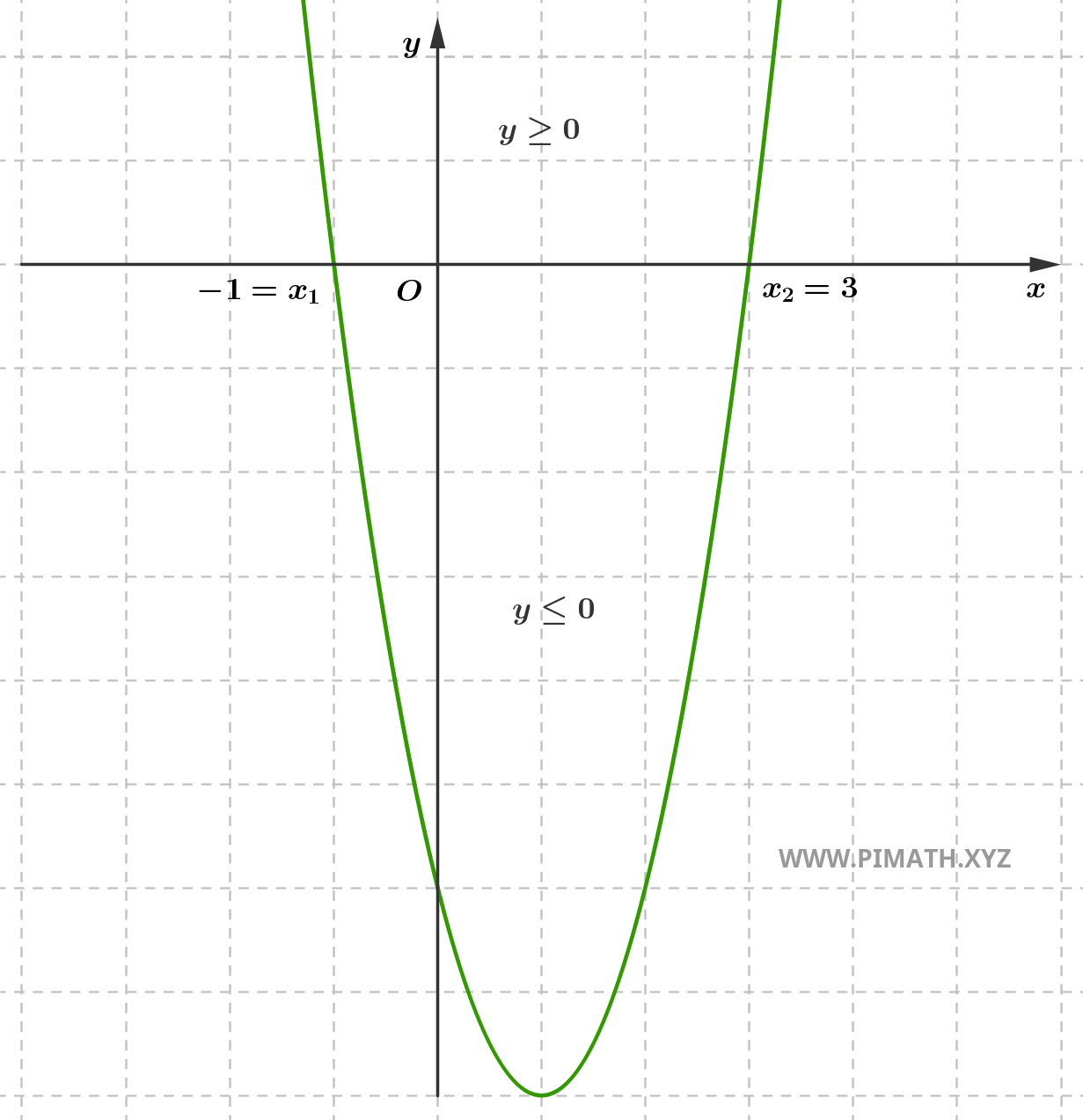
Ou então:
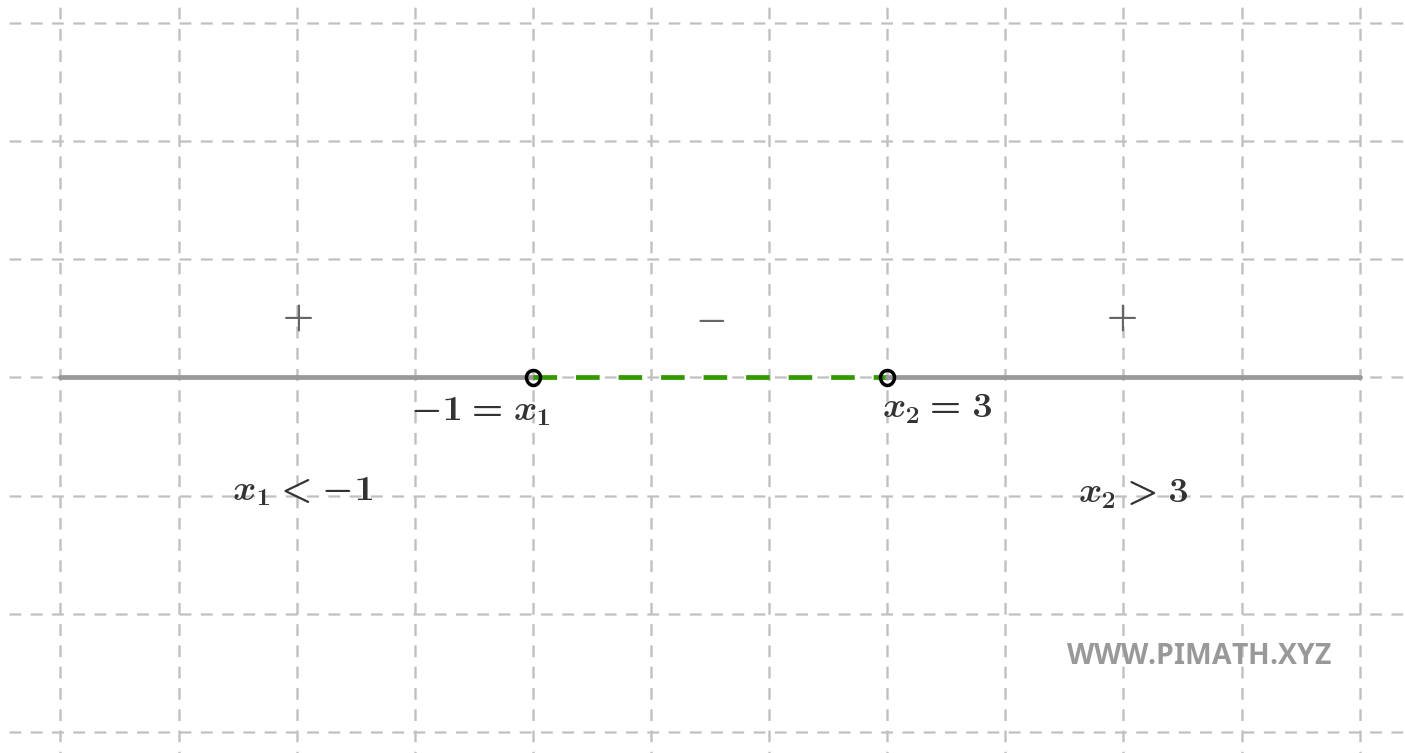
Observe, finalmente, que os círculos não estão cheios pois estamos a excluir os pontos \( x = -1 \) e \( x = 3 \).
Exercício 3. Resolver a inequação do segundo grau \( 2x^2+x+1 \leq 0 \).
Solução. A inequação apresenta-se já em forma canónica.
Calculamos o discriminante:
\[ \Delta = b^2 - 4ac \]
Substituindo \( a = 2 \), \( b = 1 \), \( c = 1 \):
\[ \Delta = (1)^2 - 4(2)(1) = 1 - 8 = -7 \]
Visto que o discriminante é negativo, a equação associada \( 2x^2+x+1 = 0 \) não tem soluções reais.
Além disso, visto que o coeficiente do termo quadrático é positivo (\( a = 2 > 0 \)), a parábola tem a concavidade voltada para cima, o que significa que o seu valor é sempre positivo para qualquer valor de \( x \).
Para uma inequação na forma \( 2x^2+x+1 \leq 0 \) com \( a > 0 \) e discriminante negativo, a inequação não tem soluções, visto que a função é sempre positiva e nunca pode ser menor ou igual a zero.
Portanto, a solução é o conjunto vazio. O gráfico da função é:
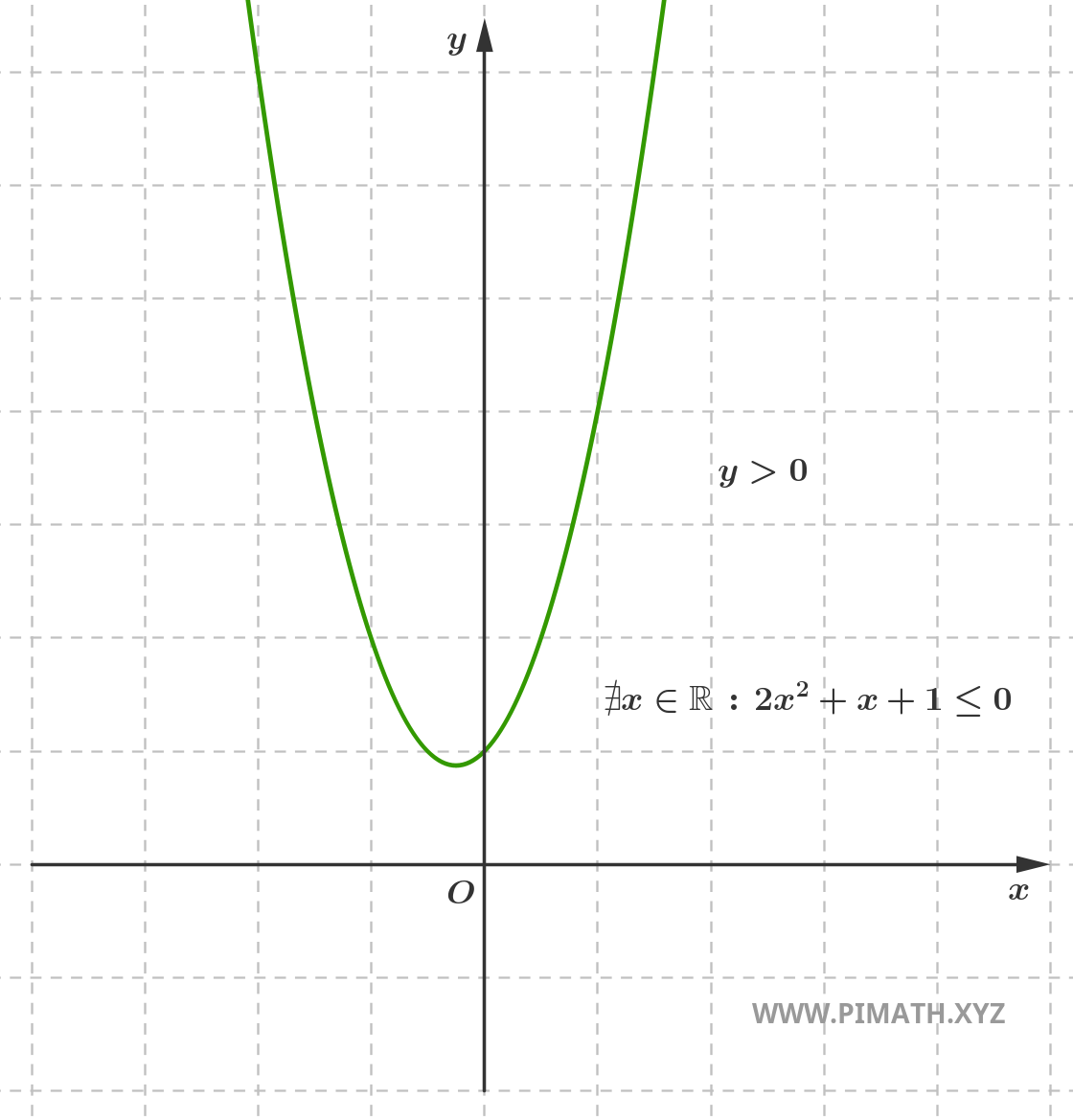
Como se pode observar, a parábola está sempre acima do eixo \( x \), portanto não há valores de \( x \) que satisfaçam a inequação \( 2x^2+x+1 \leq 0 \).

