Una inecuación de primer grado es una expresión algebraica que establece una relación de orden entre dos términos que contienen una variable lineal. Puede escribirse en la forma:
\[ a x + b \leq 0 \quad \text{o} \quad a x + b \geq 0 \]
donde \( a \) y \( b \) son coeficientes reales con \( a \neq 0 \) y \( x \) es la variable incógnita. Se habla de inecuación en sentido estricto si
\[ a x + b < 0 \quad \text{o} \quad a x + b > 0 \]
Índice
- Diferencia entre Ecuaciones e Inecuaciones de Primer Grado
- Principios de Equivalencia para las Inecuaciones
- Cómo resolver las Inecuaciones de Primer Grado
- Representación Gráfica de las Soluciones de las Inecuaciones de Primer Grado
Diferencia entre Ecuaciones e Inecuaciones de Primer Grado
Una ecuación de primer grado es una igualdad entre dos expresiones que contienen una variable lineal. Su solución está constituida por un único valor que satisface la igualdad. Una inecuación de primer grado, en cambio, define un conjunto de valores para los cuales se verifica la relación de orden. El conjunto de soluciones de una inecuación está generalmente constituido por un intervalo de números reales.
Principios de Equivalencia para las Inecuaciones
La resolución de una inecuación de primer grado se basa en tres principios fundamentales:
Primer Principio de Equivalencia
El principio de equivalencia para las inecuaciones, o principio de adición, afirma que, si se suma o resta el mismo número a ambos miembros de una inecuación, la relación de orden no cambia. Por ejemplo:
Si \( a x + b \leq 0 \), entonces podemos sumar \( c \) a ambos miembros y obtener:
\[ a x + b + c \leq c \]
Segundo Principio de Equivalencia
El segundo principio de equivalencia afirma que, si se multiplica o divide ambos miembros de una inecuación por un número positivo, la relación de orden no cambia. Sin embargo, si se multiplica o divide por un número negativo, la inecuación debe invertirse. He aquí algunos ejemplos:
Si \( a x + b \leq 0 \) y multiplicamos ambos miembros por un número positivo \( k \), obtenemos:
\[ k(a x + b) \leq k \cdot 0 \]
Si, en cambio, multiplicamos por un número negativo \( k \), la inecuación se convierte en:
\[ k(a x + b) \geq k \cdot 0 \]
Atención al Cambio del Signo de la Inecuación
Cuando se multiplica o se divide ambos miembros de una inecuación por un número negativo, es fundamental invertir el signo de la inecuación. Por ejemplo:
Si \( -3 x \leq 6 \), dividiendo ambos miembros entre \( -3 \), debemos invertir el signo de la inecuación:
\[ x \geq -2 \]
Cómo resolver las Inecuaciones de Primer Grado
La resolución de una inecuación de primer grado puede dividirse en pasos claros y sistemáticos. Los pasos generales para resolver una inecuación de primer grado son:
Pasos Generales para Resolver una Inecuación
- Aislar el término con la variable: Movemos todos los términos que no contienen la variable a un lado (normalmente el miembro derecho) de la inecuación y los términos que contienen la variable al otro lado.
- Aplicar el principio de adición o sustracción: Si es necesario, sumamos o restamos el mismo número de ambos miembros de la inecuación para aislar el término con la variable.
- Multiplicar o dividir por un coeficiente: Si la variable tiene un coeficiente numérico, dividimos ambos miembros entre el coeficiente de la variable. Si se multiplica o divide por un número negativo, recordemos invertir el signo de la inecuación.
- Verificación de la solución: Una vez aislada la variable, verificamos que la solución satisfaga la inecuación inicial.
Ejemplos Prácticos con Explicaciones Paso a Paso
Veamos ahora un ejemplo práctico de resolución de una inecuación de primer grado:
Ejemplo 1. Resuelve la inecuación \( 3x - 5 \leq 7 \).
Empecemos aplicando los pasos descritos anteriormente:
- Aislar el término con la variable: Sumamos \( 5 \) a ambos miembros para obtener: \[ 3x \leq 7 + 5 \quad \Rightarrow \quad 3x \leq 12 \]
- Dividir ambos miembros entre \( 3 \): Dividimos ambos miembros entre \( 3 \) para aislar \( x \): \[ x \leq \frac{12}{3} \quad \Rightarrow \quad x \leq 4 \]
- Verificación de la solución: La solución \( x \leq 4 \) es la respuesta final. Si sustituimos \( x = 4 \) en la inecuación original, tendríamos: \[ 3(4) - 5 = 12 - 5 = 7 \quad \Rightarrow \quad 7 \leq 7 \] Lo cual es verdadero. Por lo tanto, la solución es correcta y la representación gráfica es la siguiente:
Ejemplo 2: Resuelve la inecuación \( -2x + 3 > 7 \)
Ahora veamos otro ejemplo con un coeficiente negativo delante de la variable:
- Aislar el término con la variable: Primero restamos \( 3 \) de ambos miembros: \[ -2x > 7 - 3 \quad \Rightarrow \quad -2x > 4 \]
- Dividir ambos miembros entre \( -2 \): Cuando dividimos entre un número negativo, invertimos el signo de la inecuación: \[ x < \frac{4}{-2} \quad \Rightarrow \quad x < -2 \]
- Verificación de la solución: La solución \( x < -2 \) es correcta. Si sustituimos \( x = -3 \) (que es menor que -2), tendríamos: \[ -2(-3) + 3 = 6 + 3 = 9 \quad \Rightarrow \quad 9 > 7 \] Lo cual es verdadero. Por lo tanto, la solución es correcta y la representación gráfica es la siguiente.
Representación Gráfica de las Soluciones de las Inecuaciones de Primer Grado
Como ya hemos visto, la representación gráfica de las soluciones de una inecuación de primer grado en una recta numérica es una forma muy útil de visualizar el intervalo de soluciones. En general, la solución de una inecuación de primer grado puede representarse como un segmento o una parte de la recta numérica, dependiendo de si la desigualdad es estricta o no.
Cómo Representar las Soluciones en una Recta Numérica
Para representar las soluciones de una inecuación de primer grado en una recta numérica, sigue estos pasos:
- Identifica la solución: Una vez resuelta la inecuación, determina el intervalo de soluciones. Por ejemplo, si la solución es \( x \leq 4 \), el intervalo de soluciones es \( (-\infty, 4] \).
- Traza la recta numérica: Dibuja una recta horizontal y marca los números significativos, como los límites del intervalo de soluciones.
- Indica la solución:
- Si la inecuación es del tipo \( \leq \) o \( \geq \), indica el límite del intervalo con un círculo cerrado en la recta numérica.
- Si la inecuación es del tipo \( < \) o \( > \), indica el límite con un círculo abierto, que señala que ese punto no está incluido en la solución.
- Indica el intervalo: Traza una línea continua o discontinua para representar el intervalo de soluciones.
Interpretación Gráfica de la Solución
La interpretación gráfica de las soluciones de una inecuación en una recta numérica permite visualizar rápidamente cuál es el conjunto de valores que satisfacen la relación. He aquí algunos ejemplos de cómo se representan las soluciones:
Ejemplo 1. Solución \( x \leq 4 \)
La solución \( x \leq 4 \) implica que todos los números menores o iguales a \( 4 \) son soluciones. La representación gráfica es la siguiente:
Solución. \( x \leq 4 \).
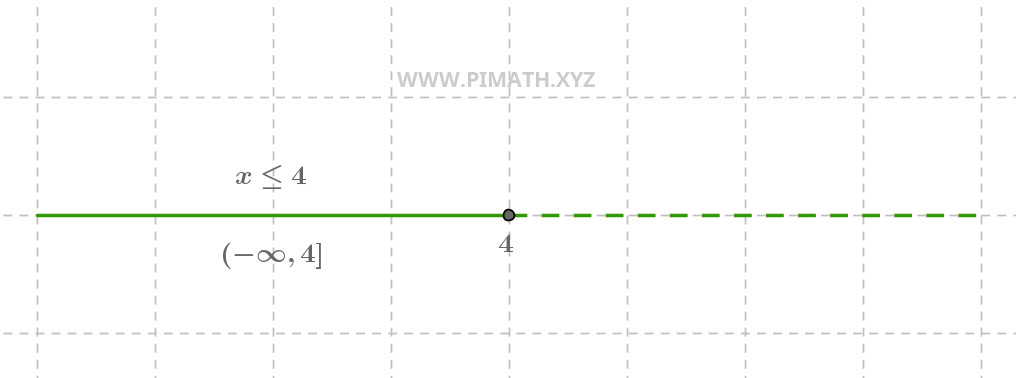
En la recta numérica, vemos un círculo cerrado en \( 4 \) (porque \( 4 \) está incluido) y una semirrecta que parte desde \( -\infty \) y va hacia \( 4 \).
Ejemplo 2. Solución \( x > -2 \).
La solución \( x > -2 \) implica que todos los números mayores que \( -2 \) son soluciones. La representación gráfica es la siguiente:
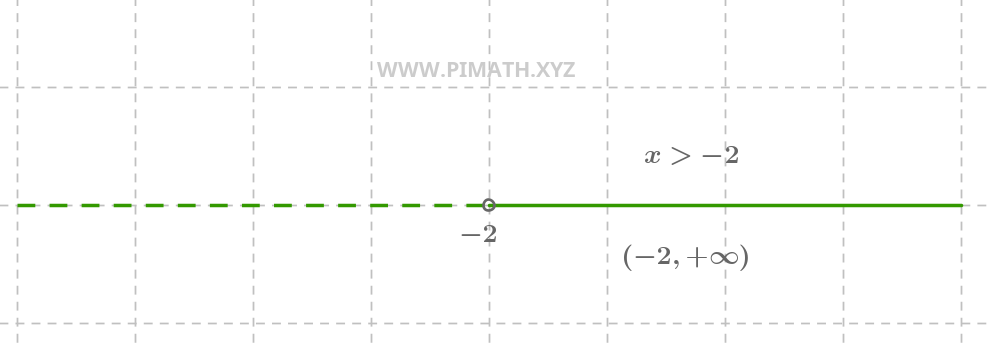
En la recta numérica, vemos un círculo abierto en \( -2 \) (porque \( -2 \) no está incluido) y una línea continua que parte desde \( -2 \) y va hacia \( +\infty \).
Ejemplo 3. Solución \( -2 \leq x < 5 \)
La solución \( -2 \leq x < 5 \) es un intervalo que incluye \( -2 \) pero excluye \( 5 \). La representación gráfica es la siguiente:
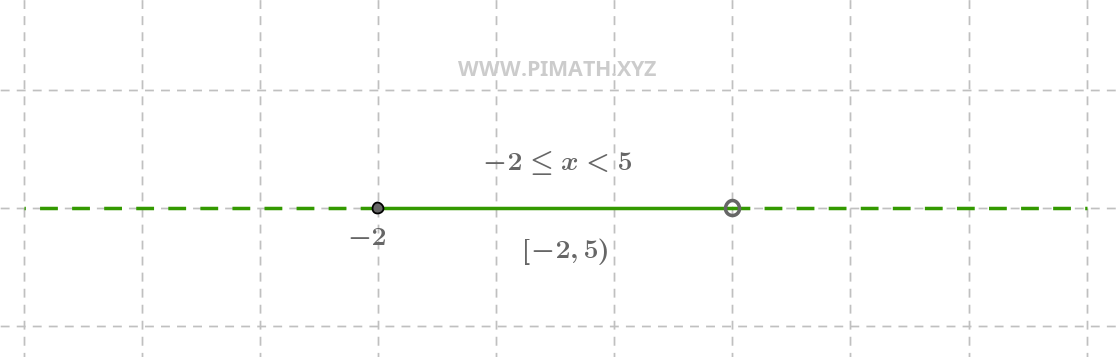
En la recta numérica, vemos un círculo cerrado en \( -2 \) y un círculo abierto en \( 5 \), con una línea continua entre ellos.
La interpretación gráfica de estas soluciones muestra visualmente qué valores satisfacen la inecuación, facilitando a quien estudia ver el conjunto de soluciones.

