El estudio de las posiciones relativas entre dos rectas es uno de los temas fundamentales de la geometría analítica plana. Comprender cómo pueden posicionarse dos rectas en el plano cartesiano permite clasificar con precisión todas las situaciones geométricas posibles: desde la intersección en un único punto hasta la superposición completa.
Índice
- Representación de las rectas en el plano
- Clasificación de las posiciones relativas
- Rectas perpendiculares
- Ejercicios resueltos
Representación de las rectas en el plano
Dadas dos rectas en el plano, pueden presentarse tres configuraciones principales:
- Rectas coincidentes: se trata de dos ecuaciones que describen en realidad la misma recta. En este caso, las rectas tienen todos los puntos en común y son indistinguibles desde el punto de vista geométrico.
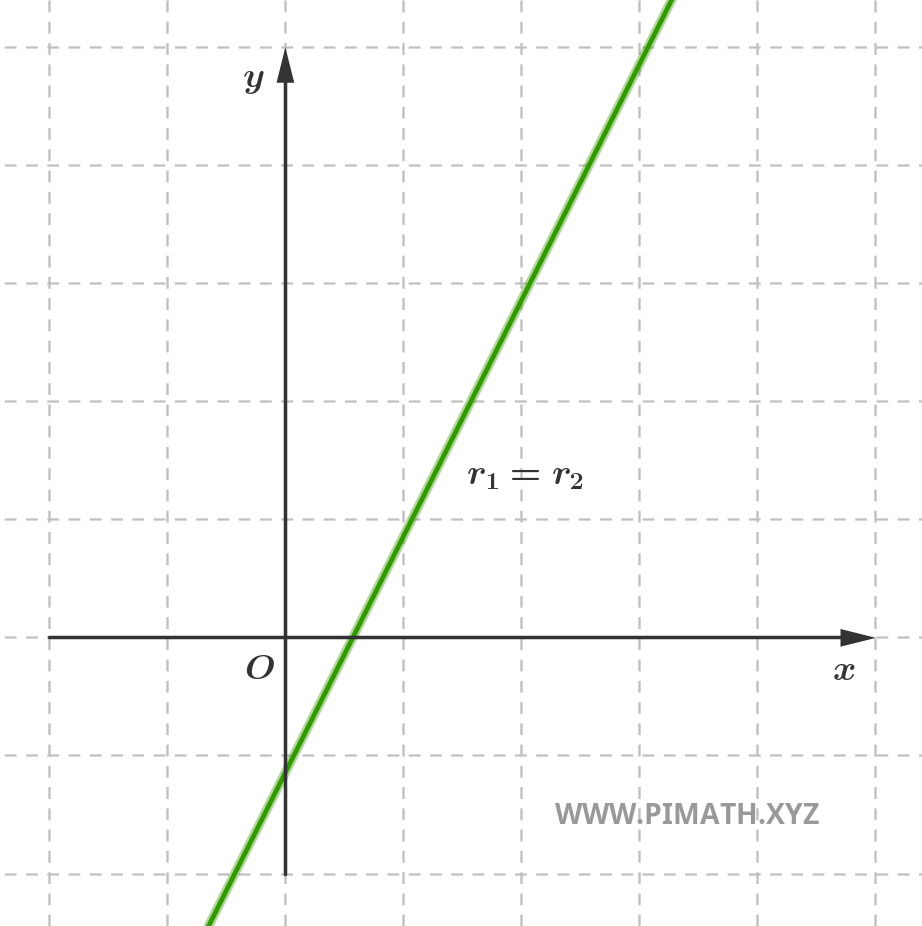
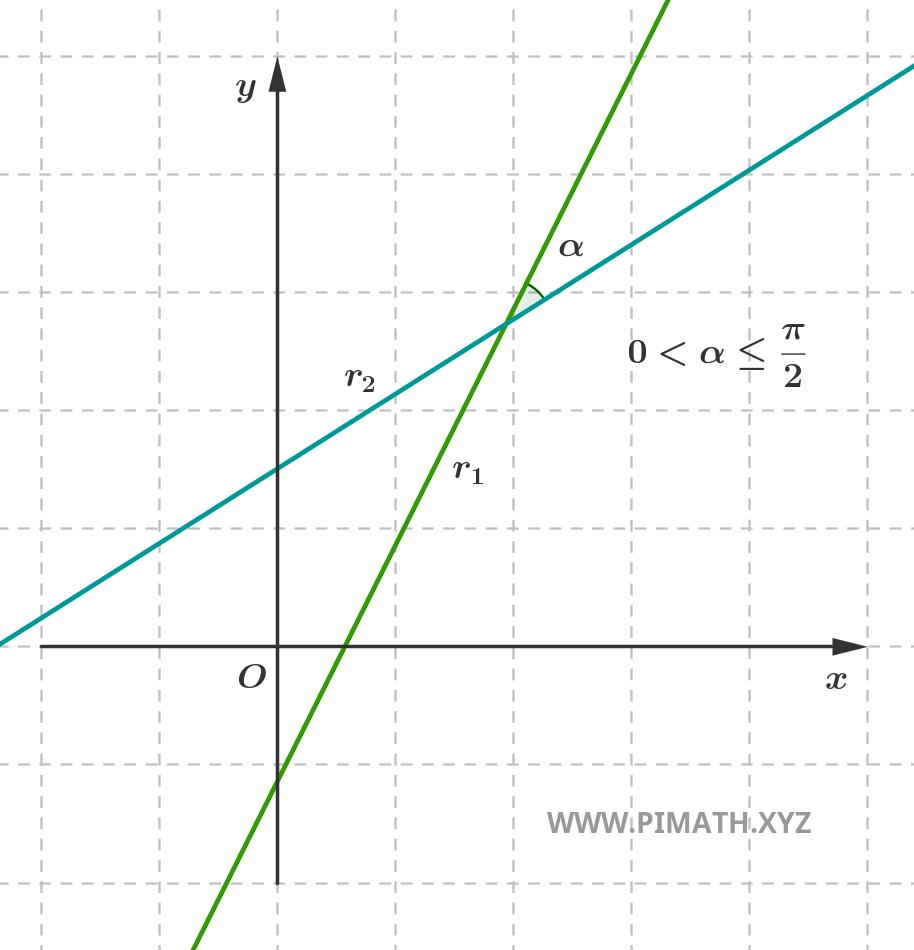
- Rectas secantes: se intersectan en un solo punto del plano, formando un ángulo que puede tomar cualquier amplitud comprendida entre 0° y 180°, excluyendo los casos de paralelismo.
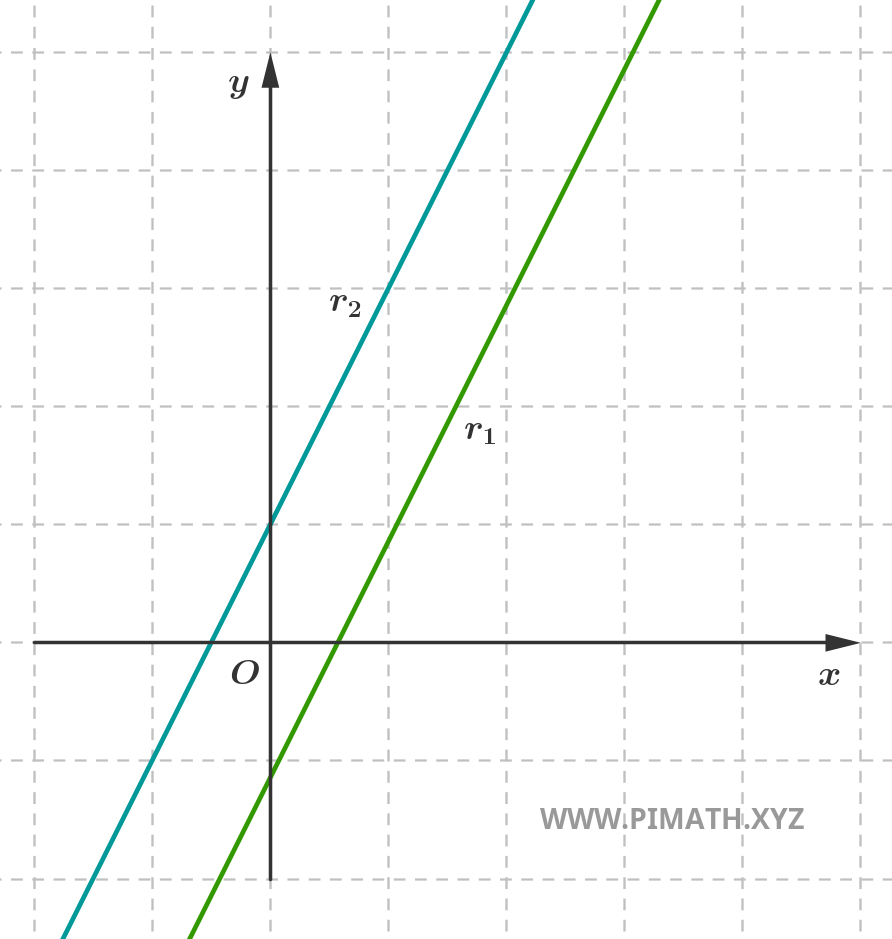
- Rectas paralelas distintas: aunque tengan la misma inclinación (es decir, el mismo coeficiente angular), estas rectas nunca se encuentran. No comparten ningún punto.
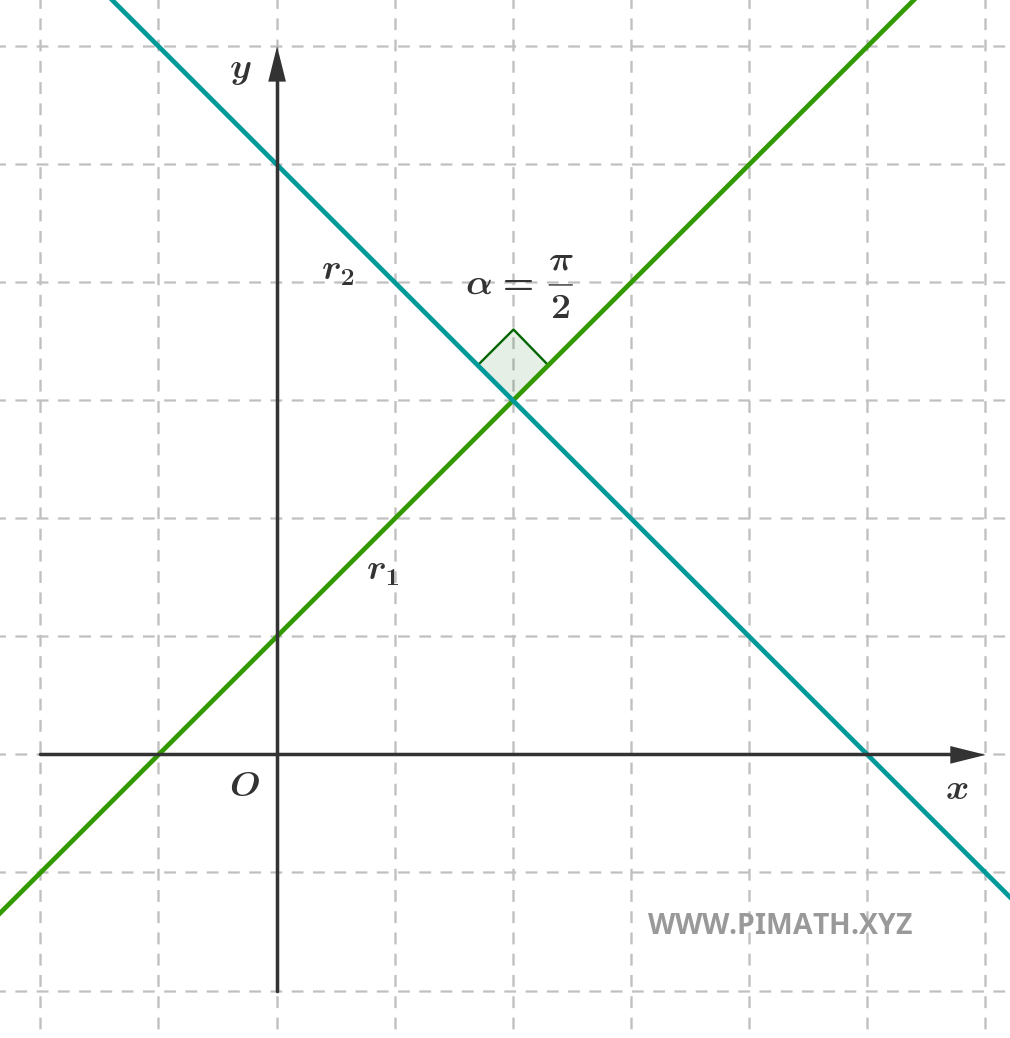
Dentro de las rectas secantes se encuentra un caso particular muy importante: el de las rectas perpendiculares. Dos rectas son perpendiculares si se intersectan formando un ángulo recto \( \displaystyle \frac{\pi}{2} \) (es decir, de 90°).
Formas de la ecuación de una recta
Una recta en el plano cartesiano puede representarse de múltiples maneras, equivalentes entre sí pero útiles en contextos diferentes.
La forma explícita, también llamada forma reducida, es quizás la más intuitiva:
\[ y = mx + q \]
En esta ecuación:
El parámetro \( m \in \mathbb{R} \) se denomina coeficiente angular o pendiente y representa la inclinación de la recta. Por convención, si la recta es vertical, se dice que el coeficiente angular es infinito o no está definido.
El término \( q \in \mathbb{R} \) es la ordenada al origen, es decir, el punto donde la recta intersecta el eje \( y \).
Otra forma de escritura es la forma implícita, también llamada forma general:
\[ ax + by + c = 0 \]
En este caso, \( a, b, c \in \mathbb{R} \), y debe cumplirse \( a^2 + b^2 \neq 0 \) para que se trate efectivamente de la ecuación de una recta.
Relación entre las formas
Cuando el coeficiente \( b \) es distinto de cero, es posible obtener la forma explícita a partir de la implícita. En efecto, resolviendo respecto a \( y \), se obtiene:
\[ ax + by + c = 0 \quad \Leftrightarrow \quad y = -\frac{a}{b}x - \frac{c}{b} \]
De este modo, el coeficiente angular resulta \( m = -\displaystyle \frac{a}{b} \) y la ordenada al origen es \( q = -\displaystyle \frac{c}{b} \).
Si en cambio \( b = 0 \) y \( a \neq 0 \), la ecuación se reduce a la forma \( x = -\displaystyle \frac{c}{a} \), que representa una recta vertical. En este caso, el coeficiente angular no está definido.
Clasificación de las posiciones relativas
Rectas coincidentes
Dos rectas son coincidentes cuando coinciden punto por punto: cada punto de una pertenece también a la otra. En esencia, se trata de la misma recta expresada con dos ecuaciones proporcionales.
Si están expresadas en forma explícita, se tiene:
\[ r: y = mx + q \quad \text{y} \quad s: y = mx + q \]
En forma implícita, dos rectas \( r: a_1x + b_1y + c_1 = 0 \) y \( s: a_2x + b_2y + c_2 = 0 \) son coincidentes si y solo si existe una constante \( k \neq 0 \) tal que:
\[ \frac{a_1}{a_2} = \frac{b_1}{b_2} = \frac{c_1}{c_2} = k \]
Equivalentemente, esto significa que \( (a_2, b_2, c_2) = k(a_1, b_1, c_1) \) para algún \( k \neq 0 \).
Ejemplo: las rectas \( 2x + 3y - 6 = 0 \) y \( 4x + 6y - 12 = 0 \) son coincidentes, porque los coeficientes de una son el doble de los de la otra:
\[ \frac{2}{4} = \frac{3}{6} = \frac{-6}{-12} = \frac{1}{2} \]
Rectas paralelas
Dos rectas son paralelas si tienen la misma dirección. En el caso de que no coincidan, se dicen paralelas distintas y no tienen puntos en común.
En forma explícita, la condición de paralelismo es:
\[ m_1 = m_2 \]
Si además \( q_1 \neq q_2 \), entonces las rectas son paralelas distintas.
En forma implícita, dos rectas \( r: a_1x + b_1y + c_1 = 0 \) y \( s: a_2x + b_2y + c_2 = 0 \) son paralelas si y solo si:
\[ a_1b_2 - a_2b_1 = 0 \]
Esto equivale a decir que \( \displaystyle \frac{a_1}{a_2} = \displaystyle \frac{b_1}{b_2} \) (cuando \( a_2, b_2 \neq 0 \)).
Para tener paralelismo distinto, se debe verificar además que:
\[ \frac{c_1}{c_2} \neq \frac{a_1}{a_2} \quad \text{(es decir} \quad \frac{c_1}{c_2} \neq \frac{b_1}{b_2}\text{)} \]
Ejemplo: las rectas \( r: y = 3x + 2 \) y \( s: y = 3x - 1 \) son paralelas distintas porque tienen el mismo coeficiente angular pero diferente ordenada al origen.
Rectas secantes
Dos rectas son secantes si se intersectan en un único punto. Esto ocurre cuando las rectas tienen direcciones diferentes, es decir, coeficientes angulares distintos (en el caso de rectas no verticales).
En forma explícita, basta verificar que:
\[ m_1 \neq m_2 \]
En forma implícita, la condición es:
\[ a_1b_2 - a_2b_1 \neq 0 \]
Punto de intersección
Para determinar el punto de intersección entre dos rectas secantes expresadas en forma implícita, se resuelve el siguiente sistema lineal:
\[ \begin{cases} a_1x + b_1y + c_1 = 0 \\ a_2x + b_2y + c_2 = 0 \end{cases} \]
Aplicando la regla de Cramer, las coordenadas del punto de intersección son:
\[ x = \frac{b_1c_2 - b_2c_1}{a_1b_2 - a_2b_1}, \quad y = \frac{a_2c_1 - a_1c_2}{a_1b_2 - a_2b_1} \]
siempre que \( a_1b_2 - a_2b_1 \neq 0 \).
Rectas perpendiculares
Condición de perpendicularidad
Dos rectas son perpendiculares si se intersectan formando un ángulo recto, es decir, de 90°.
En forma explícita, si las rectas tienen coeficientes angulares \( m_1 \) y \( m_2 \) finitos, la condición es:
\[ m_1 \cdot m_2 = -1 \]
Caso particular: una recta horizontal (\( m = 0 \)) es perpendicular a una recta vertical (coeficiente angular no definido).
En forma implícita, dos rectas \( r: a_1x + b_1y + c_1 = 0 \) y \( s: a_2x + b_2y + c_2 = 0 \) son perpendiculares si y solo si:
\[ a_1a_2 + b_1b_2 = 0 \]
Esta relación deriva del hecho de que los vectores normales de las dos rectas, \( \vec{n}_1 = (a_1, b_1) \) y \( \vec{n}_2 = (a_2, b_2) \), resultan ortogonales, es decir, su producto escalar es nulo.
Demostración analítica
El ángulo \( \theta \) entre dos rectas de coeficientes angulares \( m_1 \) y \( m_2 \) está expresado por la fórmula:
\[ \tan(\theta) = \left| \frac{m_2 - m_1}{1 + m_1m_2} \right| \]
donde \( \theta \) representa el ángulo agudo entre las dos rectas.
Si \( m_1m_2 = -1 \), el denominador \( 1 + m_1m_2 \) se anula y la tangente se vuelve indefinida, lo que corresponde a un ángulo de 90°.
Ejercicios resueltos
Ejercicio 1. Establecer si las rectas \( r: y = -2x + 1 \) y \( s: y = \displaystyle \frac{1}{2}x - 3 \) son perpendiculares.
Determinamos los coeficientes angulares:
\[ m_1 = -2 \]
\[ m_2 = \frac{1}{2} \]
Verificamos el producto entre los dos coeficientes:
\[ m_1 \cdot m_2 = (-2) \cdot \frac{1}{2} = -1 \]
Puesto que el producto es igual a -1, podemos concluir que las dos rectas son perpendiculares.
Ejercicio 2. Calcular el ángulo agudo entre las rectas \( r: y = 2x \) y \( s: y = -x \).
Los coeficientes angulares son:
\[ m_1 = 2 \]
\[ m_2 = -1 \]
Utilizamos la fórmula para el cálculo del ángulo agudo \( \theta \) entre dos rectas:
\[ \tan(\theta) = \left| \frac{m_2 - m_1}{1 + m_1 m_2} \right| = \left| \frac{-1 - 2}{1 + 2 \cdot (-1)} \right| = \left| \frac{-3}{1 - 2} \right| = \left| \frac{-3}{-1} \right| = 3 \]
Por tanto:
\[ \theta = \arctan(3) \approx 71{,}57^\circ \]
Ejercicio 3. Hallar la ecuación de la recta perpendicular a \( r: y = -\displaystyle \frac{3}{2}x + 4 \) y que pasa por el punto \( P(2, 1) \).
El coeficiente angular de la recta dada es \( m = -\displaystyle \frac{3}{2} \).
El coeficiente angular de la recta perpendicular será el opuesto del recíproco:
\[ m' = -\frac{1}{m} = -\frac{1}{-\frac{3}{2}} = \frac{2}{3} \]
Utilizamos la fórmula del haz propio de rectas que pasan por \( P(2, 1) \):
\[ y - y_0 = m'(x - x_0) \quad \text{con } (x_0, y_0) = (2, 1) \] \[ y - 1 = \frac{2}{3}(x - 2) \] \[ y = \frac{2}{3}x - \frac{4}{3} + 1 = \frac{2}{3}x - \frac{1}{3} \]
La ecuación buscada es:
\[ y = \frac{2}{3}x - \frac{1}{3} \]
Ejercicio 4. Determinar el valor de \( k \) para que las rectas \( r: 2x + 3y - 1 = 0 \) y \( s: kx + 6y + 2 = 0 \) sean paralelas.
Dos rectas en forma implícita son paralelas si \( a_1b_2 - a_2b_1 = 0 \).
Identificamos los coeficientes:
- Recta \( r \): \( a_1 = 2, b_1 = 3, c_1 = -1 \)
- Recta \( s \): \( a_2 = k, b_2 = 6, c_2 = 2 \)
Aplicamos la condición:
\[ a_1b_2 - a_2b_1 = 2 \cdot 6 - k \cdot 3 = 12 - 3k = 0 \] \[ 3k = 12 \quad \Rightarrow \quad k = 4 \]
Verificamos que para \( k = 4 \) las rectas sean efectivamente paralelas distintas:
\[ \frac{a_1}{a_2} = \frac{2}{4} = \frac{1}{2} \]
\[ \frac{b_1}{b_2} = \frac{3}{6} = \frac{1}{2} \]
\[ \frac{c_1}{c_2} = \frac{-1}{2} = -\frac{1}{2} \]
Puesto que \( \displaystyle \frac{a_1}{a_2} = \displaystyle \frac{b_1}{b_2} \neq \displaystyle \frac{c_1}{c_2} \), las rectas son paralelas distintas para \( k = 4 \).
Ejercicio 5. Determinar el punto de intersección entre las rectas:
\( r: x + 2y - 3 = 0 \)
\( s: 2x - y + 1 = 0 \)
Resolvemos el sistema:
\[ \begin{cases} x + 2y = 3 \\ 2x - y = -1 \end{cases} \]
Utilizamos el método de eliminación. Multiplicamos la segunda ecuación por 2:
\[ \begin{cases} x + 2y = 3 \\ 4x - 2y = -2 \end{cases} \]
Sumamos las dos ecuaciones:
\[ x + 4x + 2y - 2y = 3 + (-2) \] \[ 5x = 1 \quad \Rightarrow \quad x = \frac{1}{5} \]
Sustituimos en la primera ecuación:
\[ \frac{1}{5} + 2y = 3 \quad \Rightarrow \quad 2y = 3 - \frac{1}{5} = \frac{15 - 1}{5} = \frac{14}{5} \] \[ y = \frac{7}{5} \]
El punto de intersección es:
\[ \left( \frac{1}{5}, \frac{7}{5} \right) \]
Verificación: sustituyendo en ambas ecuaciones originales se obtiene la identidad \( 0 = 0 \), confirmando la corrección del resultado.

