Une inéquation du premier degré est une expression algébrique qui établit une relation d'ordre entre deux termes contenant une variable linéaire. Elle peut s'écrire sous la forme :
\[ a x + b \leq 0 \quad \text{ou} \quad a x + b \geq 0 \]
où \( a \) et \( b \) sont des coefficients réels avec \( a \neq 0 \) et \( x \) est la variable inconnue. On parle d'inéquation au sens strict si
\[ a x + b < 0 \quad \text{ou} \quad a x + b > 0 \]
Sommaire
- Différence entre Équations et Inéquations du Premier Degré
- Principes d'Équivalence pour les Inéquations
- Comment résoudre les Inéquations du Premier Degré
- Représentation Graphique des Solutions des Inéquations du Premier Degré
Différence entre Équations et Inéquations du Premier Degré
Une équation du premier degré est une égalité entre deux expressions contenant une variable linéaire. Sa solution est constituée d'une unique valeur qui satisfait l'égalité. Une inéquation du premier degré, en revanche, définit un ensemble de valeurs pour lesquelles la relation d'ordre est vérifiée. L'ensemble des solutions d'une inéquation est généralement constitué d'un intervalle de nombres réels.
Principes d'Équivalence pour les Inéquations
La résolution d'une inéquation du premier degré repose sur trois principes fondamentaux :
Premier Principe d'Équivalence
Le principe d'équivalence pour les inéquations, ou principe d'addition, affirme que, si l'on ajoute ou soustrait le même nombre aux deux membres d'une inéquation, la relation d'ordre ne change pas. Par exemple :
Si \( a x + b \leq 0 \), alors nous pouvons ajouter \( c \) aux deux membres et obtenir :
\[ a x + b + c \leq c \]
Deuxième Principe d'Équivalence
Le deuxième principe d'équivalence affirme que, si l'on multiplie ou divise les deux membres d'une inéquation par un nombre positif, la relation d'ordre ne change pas. Cependant, si l'on multiplie ou divise par un nombre négatif, l'inéquation doit être inversée. Voici quelques exemples :
Si \( a x + b \leq 0 \) et que nous multiplions les deux membres par un nombre positif \( k \), nous obtenons :
\[ k(a x + b) \leq k \cdot 0 \]
Si, au contraire, nous multiplions par un nombre négatif \( k \), l'inéquation devient :
\[ k(a x + b) \geq k \cdot 0 \]
Attention au Changement du Sens de l'Inéquation
Lorsqu'on multiplie ou divise les deux membres d'une inéquation par un nombre négatif, il est fondamental d'inverser le sens de l'inéquation. Par exemple :
Si \( -3 x \leq 6 \), en divisant les deux membres par \( -3 \), nous devons inverser le sens de l'inéquation :
\[ x \geq -2 \]
Comment résoudre les Inéquations du Premier Degré
La résolution d'une inéquation du premier degré peut être divisée en étapes claires et systématiques. Les étapes générales pour résoudre une inéquation du premier degré sont :
Étapes Générales pour Résoudre une Inéquation
- Isoler le terme contenant la variable : Nous déplaçons tous les termes qui ne contiennent pas la variable d'un côté (généralement le membre de droite) de l'inéquation et les termes qui contiennent la variable de l'autre côté.
- Appliquer le principe d'addition ou de soustraction : Si nécessaire, nous ajoutons ou soustrayons le même nombre des deux membres de l'inéquation pour isoler le terme contenant la variable.
- Multiplier ou diviser par un coefficient : Si la variable a un coefficient numérique, nous divisons les deux membres par le coefficient de la variable. Si l'on multiplie ou divise par un nombre négatif, rappelons-nous d'inverser le sens de l'inéquation.
- Vérification de la solution : Une fois la variable isolée, nous vérifions que la solution satisfait l'inéquation initiale.
Exemples Pratiques avec Explications Étape par Étape
Voyons maintenant un exemple pratique de résolution d'une inéquation du premier degré :
Exemple 1. Résoudre l'inéquation \( 3x - 5 \leq 7 \).
Commençons par appliquer les étapes décrites ci-dessus :
- Isoler le terme contenant la variable : Nous ajoutons \( 5 \) aux deux membres pour obtenir : \[ 3x \leq 7 + 5 \quad \Rightarrow \quad 3x \leq 12 \]
- Diviser les deux membres par \( 3 \) : Nous divisons les deux membres par \( 3 \) pour isoler \( x \) : \[ x \leq \frac{12}{3} \quad \Rightarrow \quad x \leq 4 \]
- Vérification de la solution : La solution \( x \leq 4 \) est la réponse finale. Si nous substituons \( x = 4 \) dans l'inéquation originale, nous aurions : \[ 3(4) - 5 = 12 - 5 = 7 \quad \Rightarrow \quad 7 \leq 7 \] Ce qui est vrai. Donc la solution est correcte et la représentation graphique est la suivante :
Exemple 2 : Résoudre l'inéquation \( -2x + 3 > 7 \)
Voyons maintenant un autre exemple avec un coefficient négatif devant la variable :
- Isoler le terme contenant la variable : D'abord nous soustrayons \( 3 \) des deux membres : \[ -2x > 7 - 3 \quad \Rightarrow \quad -2x > 4 \]
- Diviser les deux membres par \( -2 \) : Quand nous divisons par un nombre négatif, nous inversons le sens de l'inéquation : \[ x < \frac{4}{-2} \quad \Rightarrow \quad x < -2 \]
- Vérification de la solution : La solution \( x < -2 \) est correcte. Si nous substituons \( x = -3 \) (qui est inférieur à -2), nous aurions : \[ -2(-3) + 3 = 6 + 3 = 9 \quad \Rightarrow \quad 9 > 7 \] Ce qui est vrai. Donc la solution est correcte et la représentation graphique est la suivante.
Représentation Graphique des Solutions des Inéquations du Premier Degré
Comme nous l'avons déjà vu, la représentation graphique des solutions d'une inéquation du premier degré sur une droite numérique est un moyen très utile de visualiser l'intervalle de solutions. En général, la solution d'une inéquation du premier degré peut être représentée comme un segment ou une partie de la droite numérique, selon que l'inégalité est stricte ou non.
Comment Représenter les Solutions sur une Droite Numérique
Pour représenter les solutions d'une inéquation du premier degré sur une droite numérique, suivez ces étapes :
- Identifier la solution : Une fois l'inéquation résolue, déterminez l'intervalle de solutions. Par exemple, si la solution est \( x \leq 4 \), l'intervalle de solutions est \( (-\infty, 4] \).
- Tracer la droite numérique : Dessinez une droite horizontale et marquez les nombres significatifs, comme les limites de l'intervalle de solutions.
- Indiquer la solution :
- Si l'inéquation est du type \( \leq \) ou \( \geq \), indiquez la limite de l'intervalle avec un cercle fermé sur la droite numérique.
- Si l'inéquation est du type \( < \) ou \( > \), indiquez la limite avec un cercle ouvert, qui signale que ce point n'est pas inclus dans la solution.
- Indiquer l'intervalle : Tracez une ligne continue ou discontinue pour représenter l'intervalle de solutions.
Interprétation Graphique de la Solution
L'interprétation graphique des solutions d'une inéquation sur une droite numérique permet de visualiser rapidement quel est l'ensemble des valeurs qui satisfont la relation. Voici quelques exemples de la façon dont les solutions sont représentées :
Exemple 1. Solution \( x \leq 4 \)
La solution \( x \leq 4 \) implique que tous les nombres inférieurs ou égaux à \( 4 \) sont des solutions. La représentation graphique est la suivante :
Solution. \( x \leq 4 \).
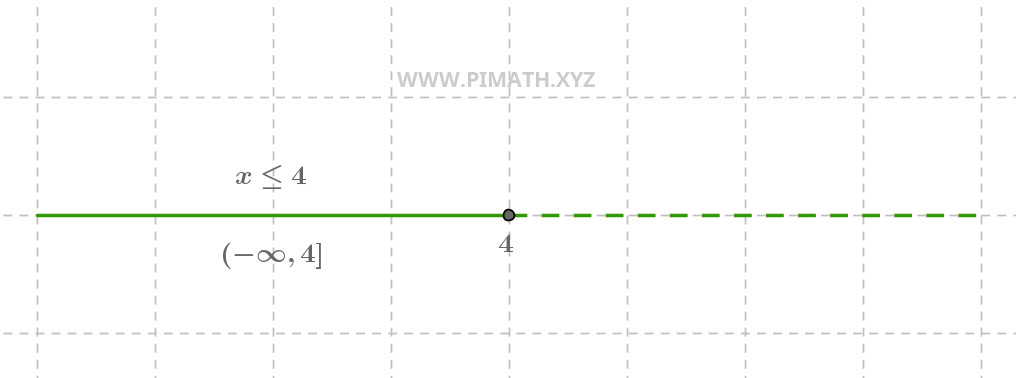
Sur la droite numérique, nous voyons un cercle fermé en \( 4 \) (parce que \( 4 \) est inclus) et une demi-droite qui part de \( -\infty \) et va vers \( 4 \).
Exemple 2. Solution \( x > -2 \).
La solution \( x > -2 \) implique que tous les nombres supérieurs à \( -2 \) sont des solutions. La représentation graphique est la suivante :
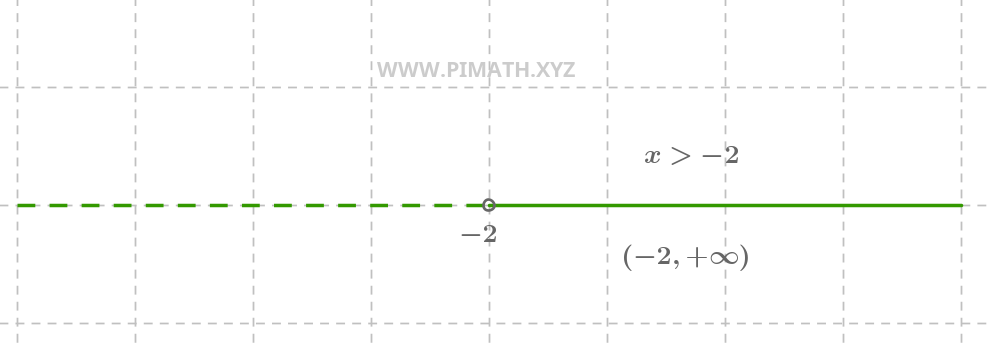
Sur la droite numérique, nous voyons un cercle ouvert en \( -2 \) (parce que \( -2 \) n'est pas inclus) et une ligne continue qui part de \( -2 \) et va vers \( +\infty \).
Exemple 3. Solution \( -2 \leq x < 5 \)
La solution \( -2 \leq x < 5 \) est un intervalle qui inclut \( -2 \) mais exclut \( 5 \). La représentation graphique est la suivante :
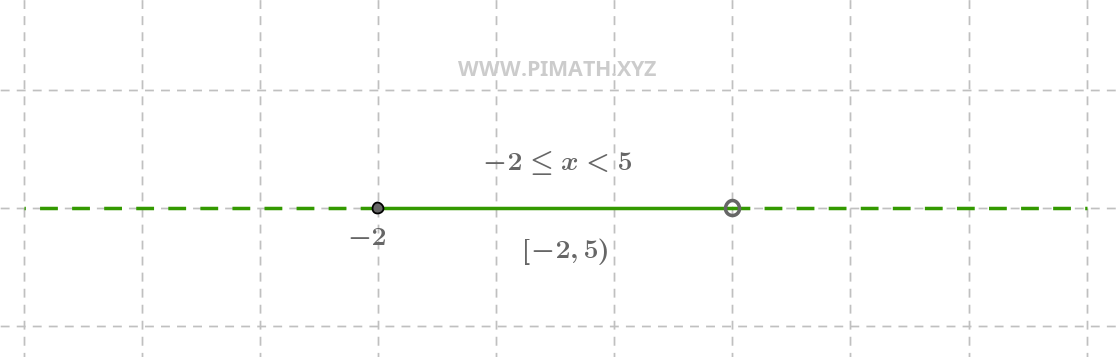
Sur la droite numérique, nous voyons un cercle fermé en \( -2 \) et un cercle ouvert en \( 5 \), avec une ligne continue entre eux.
L'interprétation graphique de ces solutions montre visuellement quelles valeurs satisfont l'inéquation, facilitant ainsi la compréhension de l'ensemble des solutions pour les étudiants.

