Il Teorema di Rolle è un risultato fondamentale applicabile alle funzioni continue e derivabili. Questo teorema stabilisce che, se una funzione \( f \) è continua in un intervallo chiuso \([a,b]\), derivabile nell'intervallo aperto \((a,b)\) e assume lo stesso valore agli estremi \( f(a) = f(b) \), allora esiste almeno un punto interno \( \xi \in (a,b) \) in cui la derivata della funzione si annulla, ossia \( f'(\xi) = 0 \). Questo risultato ha numerose applicazioni, inclusa la dimostrazione del Teorema del Valor Medio.
Indice
Teorema di Rolle
Sia \( f : [a,b] \to \mathbb{R} \) una funzione continua nell'intervallo chiuso \([a,b]\), derivabile nell'intervallo aperto \((a,b)\) e tale che \( f(a) = f(b) \). Allora esiste almeno un punto \( \xi \in (a,b) \) tale che: \[ f'(\xi) = 0 \]
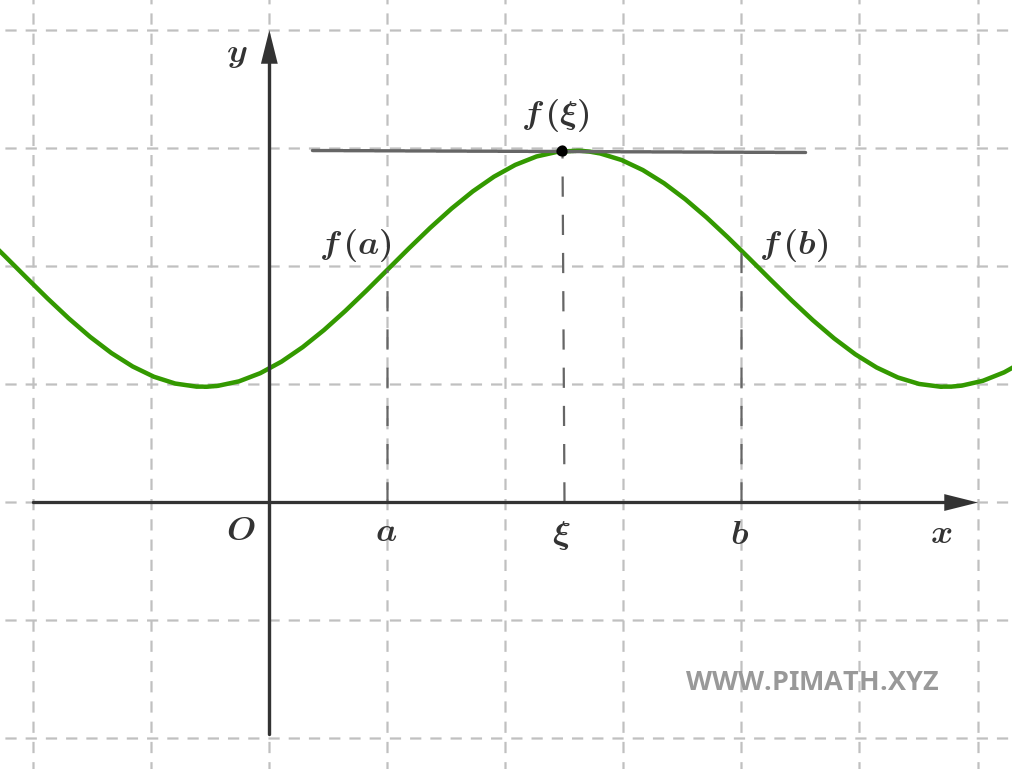
Dimostrazione. Innanzitutto, poiché \( f \) è continua su \([a,b]\), per il Teorema di Weierstrass essa ammette massimo e minimo assoluti sull'intervallo. Pertanto, esistono punti \( c, d \in [a,b] \) tali che: \[ f(c) = M \quad \text{e} \quad f(d) = m \] dove \( M = \max_{x \in [a,b]} f(x) \) e \( m = \min_{x \in [a,b]} f(x) \).
Consideriamo dapprima il caso in cui la funzione \( f \) sia costante, ovvero \( f(x) = k \) per ogni \( x \in [a,b] \). In tal caso, per definizione di derivata: \[ f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} = \lim_{h \to 0} \frac{k - k}{h} = 0 \] per ogni \( x \in (a,b) \). La tesi è dunque immediatamente verificata.
Passiamo ora al caso in cui \( f \) non sia costante. Poiché \( f(a) = f(b) \), il massimo e il minimo assoluti non possono trovarsi entrambi agli estremi \( a \) e \( b \). Deve esistere almeno un punto \( \xi \in (a,b) \) in cui \( f(\xi) = M \) oppure \( f(\xi) = m \). In entrambi i casi, \( \xi \) rappresenta un punto di massimo o minimo locale.
Sia \( \xi \) un punto di massimo locale. Per \( h \) sufficientemente piccolo:
\[ f(\xi + h) \leq f(\xi) \]
Possiamo quindi considerare i rapporti incrementali:
\[ \frac{f(\xi + h) - f(\xi)}{h} \leq 0 \quad \text{se} \ h > 0 \]
\[ \frac{f(\xi + h) - f(\xi)}{h} \geq 0 \quad \text{se} \ h < 0 \]
Dato che \( f \) è derivabile in \( \xi \), esiste il limite del rapporto incrementale, ossia: \[ f'(\xi) = \lim_{h \to 0} \frac{f(\xi + h) - f(\xi)}{h} \]
Da quanto detto sopra, abbiamo:
\[ \lim_{h \to 0^+} \frac{f(\xi + h) - f(\xi)}{h} \leq 0 \leq \lim_{h \to 0^-} \frac{f(\xi + h) - f(\xi)}{h} \]
Quindi, necessariamente: \[ f'(\xi) = 0 \]
Un ragionamento analogo si applica nel caso in cui \( \xi \) sia un punto di minimo locale.
Abbiamo così dimostrato che esiste almeno un punto \( \xi \in (a,b) \) tale che \( f'(\xi) = 0 \), completando la dimostrazione del Teorema di Rolle.

