Uma inequação do primeiro grau é uma expressão algébrica que estabelece uma relação de ordem entre dois termos que contêm uma variável linear. Pode ser escrita na forma:
\[ a x + b \leq 0 \quad \text{ou} \quad a x + b \geq 0 \]
onde \( a \) e \( b \) são coeficientes reais com \( a \neq 0 \) e \( x \) é a variável incógnita. Fala-se de inequação em sentido estrito se
\[ a x + b < 0 \quad \text{ou} \quad a x + b > 0 \]
Índice
- Diferença entre Equações e Inequações do Primeiro Grau
- Princípios de Equivalência para as Inequações
- Como resolver as Inequações do Primeiro Grau
- Representação Gráfica das Soluções das Inequações do Primeiro Grau
Diferença entre Equações e Inequações do Primeiro Grau
Uma equação do primeiro grau é uma igualdade entre duas expressões que contêm uma variável linear. A sua solução é constituída por um único valor que satisfaz a igualdade. Uma inequação do primeiro grau, por outro lado, define um conjunto de valores para os quais a relação de ordem é verificada. O conjunto de soluções de uma inequação é geralmente constituído por um intervalo de números reais.
Princípios de Equivalência para as Inequações
A resolução de uma inequação do primeiro grau baseia-se em três princípios fundamentais:
Primeiro Princípio de Equivalência
O princípio de equivalência para as inequações, ou princípio de adição, afirma que, se somarmos ou subtrairmos o mesmo número a ambos os membros de uma inequação, a relação de ordem não se altera. Por exemplo:
Se \( a x + b \leq 0 \), então podemos somar \( c \) a ambos os membros e obter:
\[ a x + b + c \leq c \]
Segundo Princípio de Equivalência
O segundo princípio de equivalência afirma que, se multiplicarmos ou dividirmos ambos os membros de uma inequação por um número positivo, a relação de ordem não se altera. Porém, se multiplicarmos ou dividirmos por um número negativo, a inequação deve ser invertida. Eis alguns exemplos:
Se \( a x + b \leq 0 \) e multiplicarmos ambos os membros por um número positivo \( k \), obtemos:
\[ k(a x + b) \leq k \cdot 0 \]
Se, pelo contrário, multiplicarmos por um número negativo \( k \), a inequação torna-se:
\[ k(a x + b) \geq k \cdot 0 \]
Atenção à Mudança do Sinal da Inequação
Quando se multiplica ou divide ambos os membros de uma inequação por um número negativo, é fundamental inverter o sinal da inequação. Por exemplo:
Se \( -3 x \leq 6 \), dividindo ambos os membros por \( -3 \), devemos inverter o sinal da inequação:
\[ x \geq -2 \]
Como resolver as Inequações do Primeiro Grau
A resolução de uma inequação do primeiro grau pode ser dividida em passos claros e sistemáticos. Os passos gerais para resolver uma inequação do primeiro grau são:
Passos Gerais para Resolver uma Inequação
- Isolar o termo com a variável: Movemos todos os termos que não contêm a variável para um lado (normalmente o membro direito) da inequação e os termos que contêm a variável para o outro lado.
- Aplicar o princípio de adição ou subtração: Se necessário, somamos ou subtraímos o mesmo número de ambos os membros da inequação para isolar o termo com a variável.
- Multiplicar ou dividir por um coeficiente: Se a variável tem um coeficiente numérico, dividimos ambos os membros pelo coeficiente da variável. Se multiplicarmos ou dividirmos por um número negativo, lembremo-nos de inverter o sinal da inequação.
- Verificação da solução: Uma vez isolada a variável, verificamos que a solução satisfaz a inequação inicial.
Exemplos Práticos com Explicações Passo a Passo
Vejamos agora um exemplo prático de resolução de uma inequação do primeiro grau:
Exemplo 1. Resolve a inequação \( 3x - 5 \leq 7 \).
Comecemos aplicando os passos descritos acima:
- Isolar o termo com a variável: Somamos \( 5 \) a ambos os membros para obter: \[ 3x \leq 7 + 5 \quad \Rightarrow \quad 3x \leq 12 \]
- Dividir ambos os membros por \( 3 \): Dividimos ambos os membros por \( 3 \) para isolar \( x \): \[ x \leq \frac{12}{3} \quad \Rightarrow \quad x \leq 4 \]
- Verificação da solução: A solução \( x \leq 4 \) é a resposta final. Se substituíssemos \( x = 4 \) na inequação original, teríamos: \[ 3(4) - 5 = 12 - 5 = 7 \quad \Rightarrow \quad 7 \leq 7 \] O que é verdadeiro. Portanto, a solução está correta e a representação gráfica é a seguinte:
Exemplo 2: Resolve a inequação \( -2x + 3 > 7 \)
Agora vejamos outro exemplo com um coeficiente negativo à frente da variável:
- Isolar o termo com a variável: Primeiro subtraímos \( 3 \) de ambos os membros: \[ -2x > 7 - 3 \quad \Rightarrow \quad -2x > 4 \]
- Dividir ambos os membros por \( -2 \): Quando dividimos por um número negativo, invertemos o sinal da inequação: \[ x < \frac{4}{-2} \quad \Rightarrow \quad x < -2 \]
- Verificação da solução: A solução \( x < -2 \) está correta. Se substituíssemos \( x = -3 \) (que é menor que -2), teríamos: \[ -2(-3) + 3 = 6 + 3 = 9 \quad \Rightarrow \quad 9 > 7 \] O que é verdadeiro. Portanto, a solução está correta e a representação gráfica é a seguinte.
Representação Gráfica das Soluções das Inequações do Primeiro Grau
Como já vimos, a representação gráfica das soluções de uma inequação do primeiro grau numa reta numérica é uma forma muito útil de visualizar o intervalo de soluções. Em geral, a solução de uma inequação do primeiro grau pode ser representada como um segmento ou uma parte da reta numérica, dependendo se a desigualdade é estrita ou não.
Como Representar as Soluções numa Reta Numérica
Para representar as soluções de uma inequação do primeiro grau numa reta numérica, siga estes passos:
- Identifique a solução: Uma vez resolvida a inequação, determine o intervalo de soluções. Por exemplo, se a solução é \( x \leq 4 \), o intervalo de soluções é \( (-\infty, 4] \).
- Trace a reta numérica: Desenhe uma reta horizontal e marque os números significativos, como os limites do intervalo de soluções.
- Indique a solução:
- Se a inequação é do tipo \( \leq \) ou \( \geq \), indique o limite do intervalo com um círculo fechado na reta numérica.
- Se a inequação é do tipo \( < \) ou \( > \), indique o limite com um círculo aberto, que assinala que esse ponto não está incluído na solução.
- Indique o intervalo: Trace uma linha contínua ou tracejada para representar o intervalo de soluções.
Interpretação Gráfica da Solução
A interpretação gráfica das soluções de uma inequação numa reta numérica permite visualizar rapidamente qual é o conjunto de valores que satisfazem a relação. Eis alguns exemplos de como as soluções são representadas:
Exemplo 1. Solução \( x \leq 4 \)
A solução \( x \leq 4 \) implica que todos os números menores ou iguais a \( 4 \) são soluções. A representação gráfica é a seguinte:
Solução. \( x \leq 4 \).
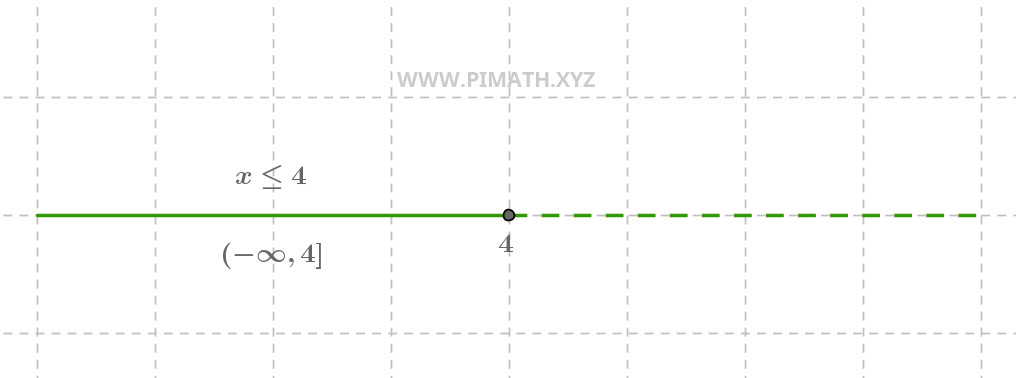
Na reta numérica, vemos um círculo fechado em \( 4 \) (porque \( 4 \) está incluído) e uma semirreta que parte de \( -\infty \) e vai até \( 4 \).
Exemplo 2. Solução \( x > -2 \).
A solução \( x > -2 \) implica que todos os números maiores que \( -2 \) são soluções. A representação gráfica é a seguinte:
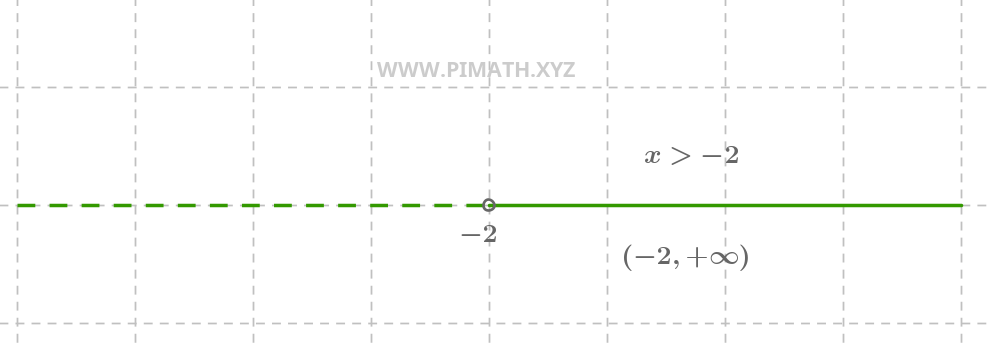
Na reta numérica, vemos um círculo aberto em \( -2 \) (porque \( -2 \) não está incluído) e uma linha contínua que parte de \( -2 \) e vai até \( +\infty \).
Exemplo 3. Solução \( -2 \leq x < 5 \)
A solução \( -2 \leq x < 5 \) é um intervalo que inclui \( -2 \) mas exclui \( 5 \). A representação gráfica é a seguinte:
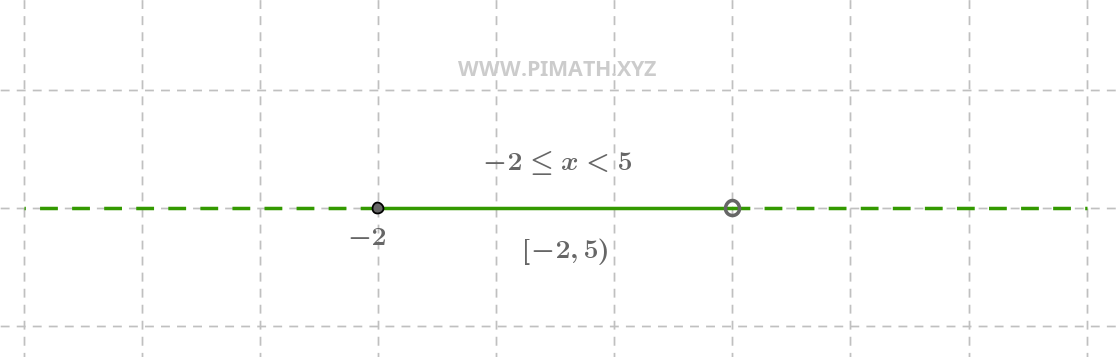
Na reta numérica, vemos um círculo fechado em \( -2 \) e um círculo aberto em \( 5 \), com uma linha contínua entre eles.
A interpretação gráfica destas soluções mostra visualmente que valores satisfazem a inequação, facilitando aos estudantes a visualização do conjunto de soluções.

